3.1 아크볼 카메라 컨트롤
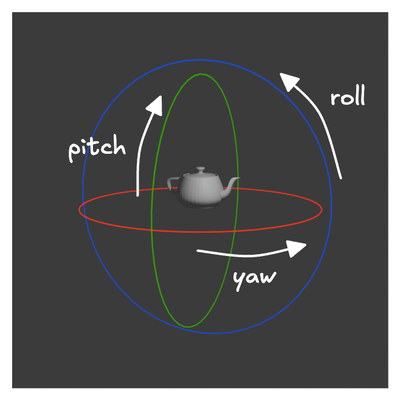
3D 렌더링에서 흔히 사용되는 또 다른 상호작용은 3D 객체를 회전하는 기능입니다. 이는 종종 아크볼(Arcball)이라는 개념을 사용하여 구현됩니다. 아이디어는 간단합니다. 3D 객체를 가상의 3D 구 안에 넣고 마우스를 사용하여 이 구를 회전시키는 것입니다. 마우스 커서는 2D 평면에서 움직이지만, 구의 3D 회전을 제어합니다. 하지만 2D 움직임이 어떻게 3D 회전을 제어할 수 있을까요? 3D 공간에서는 롤(roll), 피치(pitch), 요(yaw)의 세 가지 다른 방향으로 회전이 발생할 수 있습니다.
플레이그라운드 실행 - 3_01_arcball이를 위해 가상 구를 화면 평면에 투영합니다. 마우스 커서가 투영된 영역 내에서 움직일 때, x축 움직임은 요를 제어하고 y축 움직임은 피치를 제어합니다. 마우스 커서가 투영된 영역 밖으로 움직이면, 객체를 롤 방향으로 회전시킵니다.
이 데모에서는 구의 실루엣을 강조하는 링을 그려 투영된 구를 시각화합니다. 이 링을 렌더링하는 것은 이 책에서 여러 번 다룬 표준 작업이므로, 여기서는 자세한 설명을 생략하겠습니다. 구현 세부 사항은 샘플 코드를 참조하십시오.
이 링을 렌더링할 때 유의할 점은 파이프라인에서 기하학적 프리미티브로 라인 스트립(line-strip) 타입을 사용한다는 것입니다.
시각화를 위해 이전과 동일한 찻주전자를 렌더링하지만, 이번에는 자유롭게 회전할 수 있습니다. 역시 이전과 거의 동일하므로 자세한 내용은 생략하겠습니다.
아크볼을 위해, 우리는 그 구현을 클래스로 캡슐화합니다:
class Arcball {
constructor() {
this.radius = 5.0;
this.forwardVector = glMatrix.vec4.fromValues(this.radius, 0.0, 0.0, 0.0);
this.upVector = glMatrix.vec4.fromValues(0.0, 0.0, 1.0, 0.0);
this.currentRotation = glMatrix.mat4.create();
}
yawPitch(originalX, originalY, currentX, currentY) {
}
roll(originalX, originalY, currentX, currentY) {
}
getMatrices() {
}
}
클래스 멤버들을 설명하겠습니다. radius는 초점, 즉 회전 중심과 카메라 사이의 거리입니다. forwardVector는 카메라의 위치에서 초점까지의 시야 방향을 정의합니다. (radius, 0.0, 0.0)으로 초기화되어 카메라가 (radius, 0.0, 0.0)에서 시작하여 원점을 바라봅니다. upVector는 forwardVector에 수직이며 카메라 관점에서 위쪽을 향합니다.
currentRotation은 우리 아크볼의 회전 행렬입니다.
yawPitch(originalX, originalY, currentX, currentY) {
let originalPoint = glMatrix.vec3.fromValues(1.0, originalX, originalY);
let newPoint = glMatrix.vec3.fromValues(1.0, currentX, currentY);
let rotationAxis = glMatrix.vec3.cross(glMatrix.vec3.create(), originalPoint, newPoint);
rotationAxis = glMatrix.vec4.fromValues(rotationAxis[0], rotationAxis[1], rotationAxis[2], 0.0);
rotationAxis = glMatrix.vec4.transformMat4(glMatrix.mat4.create(), rotationAxis, this.currentRotation);
rotationAxis = glMatrix.vec3.normalize(glMatrix.vec3.create(), glMatrix.vec3.fromValues(rotationAxis[0], rotationAxis[1], rotationAxis[2]));
let sin = glMatrix.vec3.length(rotationAxis) / (glMatrix.vec3.length(originalPoint) * glMatrix.vec3.length(newPoint));
let rotationMatrix = glMatrix.mat4.fromRotation(glMatrix.mat4.create(), Math.asin(sin) * -0.03, rotationAxis);
if (rotationMatrix !== null) {
this.currentRotation = glMatrix.mat4.multiply(glMatrix.mat4.create(), rotationMatrix, this.currentRotation);
this.forwardVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.forwardVector, rotationMatrix);
this.upVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.upVector, rotationMatrix);
}
}
가장 먼저 살펴볼 함수는 요(yaw)와 피치(pitch)를 제어하는 함수입니다. 이 함수는 화면 공간에서의 원래 마우스 위치(originalX, originalY)와 현재 마우스 위치(currentX, currentY)를 두 가지 입력으로 받습니다. 초기에는 카메라가 (radius, 0, 0)에 위치하므로, 화면에 평행한 평면은 yz-평면이 됩니다. 첫 번째 단계는 화면 공간의 원래 점과 현재 점을 yz-평면으로 투영하는 것입니다: (1.0, originalX, originalY) 및 (1.0, currentX, currentY). 우리는 가상의 구의 반지름을 1로 간주하여 계산을 단순화하기 위해 (radius, ...) 대신 (1.0, ...) 좌표를 사용합니다. 이 단순화는 구의 좌표계에서 계산을 수행하기 때문에 정확성에 영향을 미치지 않습니다.
다음으로, 회전을 적용할 축을 계산해야 합니다. 이 축은 원래 벡터와 현재 벡터로 형성된 평면에 수직이므로, 두 벡터의 외적을 수행하여 얻습니다.
위 계산은 시스템에 이전 회전이 없음을 가정합니다. 즉, yz 평면이 여전히 화면 평면과 정렬되어 있다는 의미입니다. 이전에 회전이 있었다면, 이러한 회전을 회전 축에 적용해야 합니다. 마지막으로, 이 회전 축을 단위 벡터로 정규화합니다.
다음으로, 회전 각도를 얻어야 합니다. 이는 먼저 사인 값을 계산한 다음 아크사인 함수를 사용하여 유도됩니다. 최대 회전 각도는 90도 미만입니다.
마지막으로, 축과 회전 각도를 사용하여 회전 행렬을 계산합니다. 코드에서 회전 행렬이 null인지 확인하는데, 이는 원래 벡터와 현재 벡터가 매우 가까울 때 수치적 불안정성으로 인해 유효하지 않은 회전 행렬이 발생할 수 있기 때문입니다.
유효한 회전 행렬이 있다면, 기존 회전을 새 회전 행렬과 병합하고 이를 사용하여 카메라의 정방향 및 상향 벡터를 회전합니다.
roll(originalX, originalY, currentX, currentY) {
const originalVec = glMatrix.vec3.fromValues(originalX, originalY, 0.0);
const currentVec = glMatrix.vec3.fromValues(currentX, currentY, 0.0);
const crossProd = glMatrix.vec3.cross(glMatrix.vec3.create(), originalVec, currentVec);
let rad = glMatrix.vec3.dot(glMatrix.vec3.normalize(glMatrix.vec3.create(), originalVec),
glMatrix.vec3.normalize(glMatrix.vec3.create(), currentVec));
if (rad > 1.0) {
// cross product can be larger than 1.0 due to numerical error
rad = Math.PI * Math.sign(crossProd[2]);
}
else {
rad = Math.acos(rad) * Math.sign(crossProd[2]);
}
let rotationMatrix = glMatrix.mat4.fromRotation(glMatrix.mat4.create(), -rad, this.forwardVector);
if (rotationMatrix !== null) {
this.currentRotation = glMatrix.mat4.multiply(glMatrix.mat4.create(), rotationMatrix, this.currentRotation);
this.upVector = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), this.upVector, rotationMatrix);
}
}
두 번째로 살펴볼 함수는 롤(roll) 함수입니다. 이 함수는 마우스 커서가 링 밖으로 드래그될 때 트리거됩니다. 롤링의 경우, 회전 축은 항상 화면 평면에 수직이며, 뷰어를 향하거나 멀어지는 방향을 가리킵니다. 따라서 우리는 화면 평면의 좌표에서 계산을 수행하며, 원래 벡터와 현재 벡터를 각각 (originalX, originalY, 0.0) 및 (currentX, currentY, 0.0)으로 만듭니다.
회전 축을 얻기 위해 외적을 계산합니다. 이상적으로 이 축은 (0, 0, 1) 또는 (0, 0, -1)이어야 하지만, 회전 방향을 결정하는 데는 마지막 구성 요소만 중요합니다.
회전 각도는 내적과 아크코사인 함수를 사용하여 계산합니다. 수치 오류로 인해 내적이 1보다 약간 커질 수 있으며, 이 경우 아크코사인 함수가 NaN을 반환하게 됩니다. 이를 방지하기 위해, 이런 경우에는 회전 각도를 \pi 또는 -\pi로 처리합니다. 그렇지 않으면, 각도에 아크코사인 값을 사용하고 회전 축의 마지막 구성 요소의 부호를 사용하여 방향을 결정합니다.
마지막으로, 회전 각도를 회전 행렬로 변환합니다. 계산은 화면 평면에서 수행되지만, 카메라의 좌표계에서 회전을 적용합니다. 롤링의 회전 축은 카메라의 정방향 벡터와 동일하므로, 정방향 벡터와 회전 각도를 사용하여 회전 행렬을 생성합니다.
회전 행렬을 얻으면, 기존 회전을 새 회전 행렬과 병합하고, 롤링은 forwardVector를 변경하지 않으므로 upVector를 업데이트합니다.
getMatrices() {
let modelViewMatrix = glMatrix.mat4.lookAt(glMatrix.mat4.create(),
glMatrix.vec3.fromValues(this.forwardVector[0], this.forwardVector[1], this.forwardVector[2]),
glMatrix.vec3.fromValues(0, 0, 0), glMatrix.vec3.fromValues(this.upVector[0], this.upVector[1], this.upVector[2]));
return modelViewMatrix;
}
마지막으로, 아크볼 클래스에서 업데이트된 정방향 및 상향 벡터에 따라 modelViewMatrix를 가져오는 함수가 필요합니다. 이는 glMatrix에서 제공하는 lookAt 헬퍼 함수를 호출하여 달성할 수 있습니다. 3D 객체를 렌더링할 때, 이 함수를 호출하여 modelViewMatrix를 가져오기만 하면 됩니다.
다음으로, 마우스 이벤트를 어떻게 처리하는지 살펴보겠습니다:
let prevX = 0.0;
let prevY = 0.0;
let isDragging = false;
const yawPitch = 1;
const roll = 2;
canvas.onmousedown = (event) => {
var rect = canvas.getBoundingClientRect();
const x = event.clientX - rect.left;
const y = event.clientY - rect.top;
const width = rect.right - rect.left;
const height = rect.bottom - rect.top;
let radius = width;
if (height < radius) {
radius = height;
}
radius *= 0.5;
const originX = width * 0.5;
const originY = height * 0.5;
prevX = (x - originX) / radius;
prevY = (originY - y) / radius;
if ((prevX * prevX + prevY * prevY) < 0.64) {
isDragging = yawPitch;
}
else {
isDragging = roll;
}
}
마우스다운 이벤트 핸들러에서 우리의 주된 목표는 yawPitch 또는 roll 중 어떤 종류의 움직임인지 결정하는 것입니다. 커서가 투영된 구 안에 있으면 요와 피치를 수행하고, 밖에 있으면 롤을 수행한다는 것을 기억하십시오. 이 함수가 섹션별로 어떤 작업을 하는지 설명하겠습니다:
var rect = canvas.getBoundingClientRect();
const x = event.clientX - rect.left;
const y = event.clientY - rect.top;
const width = rect.right - rect.left;
const height = rect.bottom - rect.top;
이 줄들은 캔버스 내 마우스 커서 위치를 얻는 일반적인 공식으로, 왼쪽 상단 모서리를 원점으로 사용합니다.
let radius = width;
if (height < radius) {
radius = height;
}
radius *= 0.5;
이 줄들은 너비와 높이 중 더 작은 값을 선택하여 절반으로 나누고, 이를 반지름으로 사용합니다. 이는 투영된 구가 화면 영역 내에 맞도록 하여 반지름이 화면의 짧은 변만큼 커질 수 있도록 하기 위함입니다.
const originX = width * 0.5;
const originY = height * 0.5;
prevX = (x - originX) / radius;
prevY = (originY - y) / radius;
이 줄들은 좌표계를 왼쪽 상단 모서리를 원점으로 사용하는 방식에서 화면 평면의 중앙을 원점으로 사용하는 방식으로 변환합니다. 캔버스 좌표계는 y축이 아래를 향하는 반면, 화면 좌표계는 위를 향하기 때문에 Y축을 뒤집습니다.
또한 캔버스 크기에 회전 감도가 영향을 받지 않도록 반지름으로 좌표를 정규화합니다.
if ((prevX * prevX + prevY * prevY) < 0.64) {
isDragging = yawPitch;
}
else {
isDragging = roll;
}
마지막으로, 마우스 커서에서 화면 중앙까지의 거리를 계산하고, 0.64라는 고정된 임계값을 사용하여 회전 유형을 결정합니다. 커서가 캔버스 짧은 변의 0.8 이내에 있으면 요와 피치로 간주하고, 그렇지 않으면 롤로 간주합니다.
canvas.onmousemove = (event) => {
if (isDragging != 0) {
if (isDragging == yawPitch) {
arcball.yawPitch(prevX, prevY, currX, currY);
}
else if (isDragging == roll) {
arcball.roll(prevX, prevY, currX, currY);
}
prevX = currX;
prevY = currY;
requestAnimationFrame(render);
}
}
canvas.onmouseup = (event) => {
isDragging = 0;
}
다음으로, mousemove 함수를 살펴보겠습니다. 위 함수 스니펫에서 생략된 부분은 mousedown 함수와 유사하므로, 여기서는 차이점만 보여드립니다. 이전에 결정된 회전 유형에 따라 해당하는 회전 함수를 호출합니다. 그 후, 새 프레임을 렌더링하도록 요청합니다.
렌더링 코드는 특별한 것이 없으므로 생략하겠습니다. 렌더링을 위해 해야 할 일은 아크볼 클래스에서 최신 modelViewMatrix를 가져와 노멀 행렬과 같은 필요한 모든 유니폼 버퍼를 업데이트하는 것입니다.