5.8 가우시안 스플래팅

가우시안 스플래팅(Gaussian Splatting)은 작년부터 상당한 주목을 받아왔으며, 특히 이 논문 이후 더욱 그러합니다. 이 기술은 3D 사진 구현을 위한 표준 접근 방식이 될 잠재력 때문에 저의 관심을 끌었습니다.

전통적인 컴퓨터 그래픽스는 주로 삼각형을 사용하여 3D 장면을 표현하며, GPU 하드웨어는 많은 양의 삼각형을 효율적으로 렌더링하도록 최적화되어 있습니다. 다양한 각도에서 촬영된 일련의 사진에서 사실적인 3D 장면을 재구성하려는 연구는 활발한 연구 분야였습니다. 그러나 사실적인 표현을 달성하는 것은 여전히 어려운 과제입니다. 삼각형은 구름이나 머리카락처럼 모호하고 투명하거나 비정형적인 객체를 표현하는 데는 한계가 있습니다.

최근 몇 년 동안 신경 방사 필드(neural radiance fields)와 같은 암시적 3D 표현에서 진전이 있었습니다. 이러한 방법은 사실적인 결과를 생성하고 비정형 객체를 잘 처리할 수 있지만, 엄청난 계산량과 느린 렌더링 속도라는 단점이 있습니다. 이후 연구자들은 이러한 접근 방식 간의 격차를 해소할 수 있는 새로운 솔루션을 모색해 왔습니다. 가우시안 스플래팅은 잠재적인 솔루션으로 부상하고 있습니다. 그러나 이 분야는 빠르게 발전하고 있으며, 가우시안 스플래팅의 일부 한계를 해결하려는 새로운 방법들이 계속해서 나오고 있습니다. 그럼에도 불구하고 가우시안 스플래팅을 깊이 이해하는 것은 많은 미래 방법의 기반이 될 수 있으므로 가치 있는 일입니다.

이 튜토리얼에서는 가우시안 스플랫을 렌더링하는 방법과 그 수학적 의미를 알아보겠습니다. 다른 챕터와 마찬가지로, 수학적 엄밀성보다는 직관적인 이해를 강조하고자 합니다. 복잡한 개념을 이해하는 데는 직관이 중요하다고 생각하기 때문입니다. 이 방법의 공식적인 설명에 관심 있는 분들을 위해 추가 자료를 추천해 드리겠습니다. 또한, Three.js의 GaussianSplats3D 참조 구현에서 많은 도움을 받았습니다. 이 프로젝트를 꼭 확인해 보시길 강력히 권합니다.

표면 스플래팅[SOURCE]

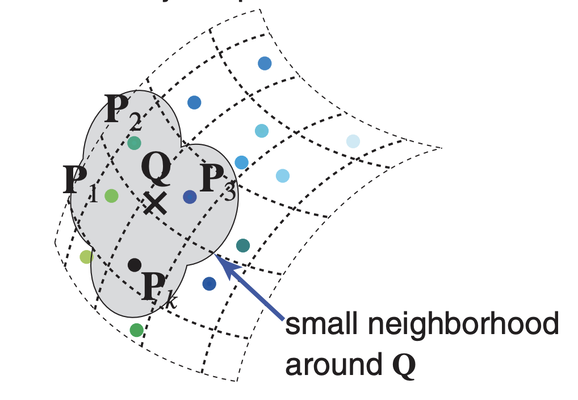
가우시안 스플래팅이란 무엇일까요? 앞서 언급했듯이, 삼각형은 가장 일반적으로 사용되는 그래픽 요소이지만, 렌더링의 기본으로 삼각형 대신 다른 프리미티브를 사용하려는 시도가 있었습니다. 예를 들어, 포인트는 또 다른 일반적인 선택이었습니다. 포인트는 명시적인 연결성을 요구하지 않으므로, 3D 스캐너나 LiDAR를 사용하여 캡처된 장면처럼 연결성을 파악하기 어려운 3D 장면을 표현할 때 유용합니다. 그러나 포인트는 크기가 없습니다. 가까이서 보면 포인트가 표면을 덮을 만큼 충분히 밀집되어 있지 않을 수 있습니다. 이 문제를 해결하기 위한 한 가지 아이디어는 포인트 대신 표면 스플랫(surface splats)이라고 불리는 작은 디스크를 렌더링하는 것입니다. 디스크는 크기를 가질 수 있으므로, 크기를 조절하여 구멍을 메울 수 있습니다. 디스크는 일반적으로 단색이 아니라 가우시안에 의해 정의된 가장자리에서 색상이 흐려지는 형태를 가집니다. 이는 인접한 디스크를 혼합하여 부드러운 전환을 만드는 데 유용합니다.

볼륨 렌더링된 흐릿한 객체[SOURCE]

또 다른 일반적인 선택은 볼륨 렌더링이라고 불립니다. 볼륨은 빛을 흡수하는 3D 픽셀로 볼 수 있는 복셀의 3D 그리드입니다. 카메라에서 광선을 발사하여 광선과 복셀 간의 교차점을 테스트하고, 각 광선을 따라 색상 값을 혼합합니다. 복셀 렌더링은 흐릿한 표면을 표현하는 데 탁월하지만, 볼륨을 저장하는 전통적인 방식은 매우 비용이 많이 듭니다.

가우시안 스플래팅은 이 두 가지의 하이브리드라고 볼 수 있습니다. 각 렌더링 요소는 3D 가우시안 함수, 즉 블랍입니다. 표면 스플랫과 유사하게 위치와 크기를 가집니다. 그러나 표면 스플랫과 달리 가우시안 스플랫은 2D뿐만 아니라 볼륨도 가집니다. 또한, 가우시안 스플랫은 모양을 가집니다. 기본 모양은 구형이지만, 임의의 타원체로 늘리거나 회전할 수 있습니다. 가우시안 스플랫에 정의된 색상도 정의된 가우시안 함수에 따라 흐려지며, 이는 표면 스플랫과 유사합니다. 가우시안 스플래팅은 앞서 언급된 두 가지 접근 방식의 장점을 결합합니다. 연결성이 필요 없으며, 희소하고, 흐릿한 표면을 표현할 수 있습니다.

가우시안 스플래팅은 작년에 이 논문을 통해 인기를 얻었지만, 이 개념은 새로운 것이 아니며, 렌더링 부분은 이 논문에서 처음 언급되었습니다. 과정을 요약하면, 많은 가우시안 스플랫으로 구성된 장면이 주어졌을 때, 먼저 일반적인 렌더링 과정에서 정점에 적용하는 것과 유사하게 일련의 회전 및 스케일링을 수행합니다. 그런 다음, 이 스플랫들은 2D 가우시안으로 화면에 투영됩니다. 마지막으로, 앞에서 뒤로 혼합을 적용하기 위해 깊이에 따라 정렬됩니다.

이 개념을 시각화하는 데 어려움이 있다면, 위에 링크된 유튜브 비디오를 시청하여 더 명확한 이해를 얻는 것을 추천합니다.

이 챕터는 지금까지 가장 복잡합니다. 따라서 단계별 접근 방식을 따를 것입니다. 렌더링 부분에 뛰어들기 전에 먼저 몇 가지 기본 사항을 다루겠습니다.

첫째, 데모를 위해 이 파일에서 데이터를 로드할 것이므로 가우시안 스플래팅의 데이터 형식에 대해 논의할 것입니다. 둘째, 로드된 데이터를 포인트 클라우드로 렌더링할 것입니다. 이를 통해 데이터가 올바르게 로드되었는지 확인할 수 있습니다. 셋째, 전체 장면을 렌더링하는 대신 단일 가우시안 스플랫을 렌더링할 것입니다. 이는 기본 수학을 이해하는 데 도움이 될 것이므로 가장 중요한 부분입니다. 마지막으로, 이전 챕터의 기수 정렬 알고리즘을 포함하여 배운 모든 것을 결합하여 전체 장면을 렌더링할 것입니다.

이 챕터는 가우시안 스플래팅의 렌더링에 중점을 둡니다. 하지만 가우시안 스플랫이 어떻게 생성되는지에 대해 간략히 다룰 필요가 있습니다. 일반적으로 가우시안 스플랫 장면은 다양한 각도에서 찍은 사진으로 생성됩니다. 직접 설정하고 싶다면 공식 가우시안 스플래팅 저장소를 방문할 수 있습니다. 또는 Polycam과 같은 온라인 도구를 사용하여 이미지를 업로드한 후 가우시안 스플랫 장면을 생성할 수 있습니다.

가우시안 스플랫에는 두 가지 주요 데이터 형식이 있습니다. 하나는 포인트 클라우드에 사용되는 PLY 파일입니다. PLY 파일은 매우 유연하며, 내용의 형식을 설명하는 사람이 읽을 수 있는 헤더와 실제 데이터가 포함된 바이너리 섹션으로 구성됩니다.

또 다른 일반적인 형식은 .splat 파일입니다. 이 형식은 연속적인 가우시안의 간단한 바이너리입니다. 형식은 다음과 같이 설명할 수 있습니다:

• XYZ - 위치 (Float32)

• XYZ - 스케일 (Float32)

• RGBA - 색상 (uint8)

• IJKL - 쿼터니언/회전 (uint8)

이 튜토리얼에서는 Polycam에서 생성된 PLY 파일을 사용할 것입니다. 아래는 PLY 파일의 헤더입니다:

ply
format binary_little_endian 1.0
element vertex 81946
property float x
property float y
property float z
property float nx
property float ny
property float nz
property float f_dc_0
property float f_dc_1
property float f_dc_2
property float f_rest_0
...
property float f_rest_44
property float opacity
property float scale_0
property float scale_1
property float scale_2
property float rot_0
property float rot_1
property float rot_2
property float rot_3
end_header

헤더는 대부분 이해할 수 있지만, 그리 명확하지 않은 일부 필드에 대해 설명하고자 합니다. 여기서 f_{dc}는 가우시안의 색상을 나타내고, `rot`는 회전 쿼터니언입니다. 이 파일을 JavaScript에서 직접 파싱하는 대신, C++에서 PLY 파일을 전처리하여 로드하기 쉬운 JSON 파일을 생성할 것입니다. 이 작업을 위해 직접 파일 파서를 작성할 필요 없이 happly 프로젝트를 사용할 것입니다.

happly::PLYData plyIn("../../../data/food.ply");
std::vector opacity = plyIn.getElement("vertex").getProperty("opacity");
std::vector scale0 = plyIn.getElement("vertex").getProperty("scale_0");
std::vector scale1 = plyIn.getElement("vertex").getProperty("scale_1");
std::vector scale2 = plyIn.getElement("vertex").getProperty("scale_2");
std::vector rot0 = plyIn.getElement("vertex").getProperty("rot_0");
std::vector rot1 = plyIn.getElement("vertex").getProperty("rot_1");
std::vector rot2 = plyIn.getElement("vertex").getProperty("rot_2");
std::vector rot3 = plyIn.getElement("vertex").getProperty("rot_3");
std::vector x = plyIn.getElement("vertex").getProperty("x");
std::vector y = plyIn.getElement("vertex").getProperty("y");
std::vector z = plyIn.getElement("vertex").getProperty("z");
std::vector f_dc_0 = plyIn.getElement("vertex").getProperty("f_dc_0");
std::vector f_dc_1 = plyIn.getElement("vertex").getProperty("f_dc_1");
std::vector f_dc_2 = plyIn.getElement("vertex").getProperty("f_dc_2");
std::ofstream outputFile;
outputFile.open("food.json");
outputFile << "[";
for (int i = 0; i < opacity.size(); ++i)
{

    const double SH_C0 = 0.28209479177387814;

    outputFile << "{\"p\":[" << x[i] << ", " << y[i] << ", " << z[i] << "]," << std::endl;
    outputFile << "\"r\":[" << rot0[i] << ", " << rot1[i] << ", " << rot2[i] << "," << rot3[i] << "]," << std::endl;
    outputFile << "\"c\":[" << (0.5 + SH_C0 * f_dc_0[i]) << ", " << (0.5 + SH_C0 * f_dc_1[i]) << ", " << (0.5 + SH_C0 * f_dc_2[i]) << "]," << std::endl;

    outputFile << "\"s\":[" << exp(scale0[i]) << ", " << exp(scale1[i]) << ", " << exp(scale2[i]) << "]," << std::endl;
    outputFile << "\"o\":" << (1.0 / (1.0 + exp(-opacity[i]))) << "}";

    if (i != opacity.size() - 1)
    {
        outputFile << "," << std::endl;
    }
}
outputFile << "]";

happly는 매우 사용하기 쉬운 라이브러리입니다. 필드 이름을 제공하기만 하면 해당 필드의 값 목록을 반환합니다. 스케일 및 불투명도에 대한 데이터 변환을 수행해야 한다는 점에 유의하십시오. 이 필드에 대한 공식 문서는 찾을 수 없었으므로, 이 공식은 참조 소스 코드에서 가져왔습니다.

하지만 색상 변환에 대해 설명하고자 합니다. 이 방정식은 특히 각 색상 채널에 적용되는 상수가 이상하게 보일 수 있습니다. 많은 컴퓨터 그래픽스 문제에서 우리는 구면의 복잡한 함수를 모델링해야 합니다. 예를 들어, 3D 공간의 위치에서 빛은 다양한 강도로 모든 방향에서 올 수 있습니다. 주어진 3D 방향에 대해 빛의 강도를 반환하는 함수를 찾아야 합니다. 이것은 구면에서 정의된 일반적인 함수입니다. 함수가 복잡할 수 있으므로 간단한 형태로 표현하기 어려울 수 있습니다. 한 가지 해결책은 이를 일련의 더 간단한 함수의 합으로 분해하는 것입니다. 이 기술을 구면 조화 함수(spherical harmonics)라고 합니다. 이는 푸리에 변환과 유사하지만, 각 구성 요소는 구면 함수입니다.

구면 조화 함수는 가우시안 스플래팅이 고반사 표면을 모델링하는 데 중요합니다. 거울이나 크롬 금속과 같은 표면의 경우, 보는 각도에 따라 그 모양이 변할 수 있습니다.

구면 조화 함수에 대한 자세한 설명은 이 책의 범위를 벗어납니다. 핵심은 상수 SH_{C0}가 구면 조화 함수 공식의 첫 번째 계수라는 것입니다. 구면 조화 함수로 색상을 도출했음에도 불구하고, 색상이 또한 상수이기 때문에 색상과 시야 방향을 연결하는 것처럼 보이지 않습니다. 이는 정확합니다. 이 예시에서는 각 가우시안에 대해 상수 색상을 가정하고 있으며, 이는 반사 표면을 잘 모델링할 수 없다는 것을 의미합니다.

우리는 보수적인 자세로 렌더링 과정을 단계별로 완료하고자 합니다. 첫 번째 단계는 단순히 데이터를 포인트 클라우드로 렌더링하는 것입니다. 이제 우리에게는 이것이 간단해야 합니다. 셰이더 코드는 다음과 같습니다:

@group(0) @binding(0)
var modelView: mat4x4;
@group(0) @binding(1)
var projection: mat4x4;

struct VertexOutput {
    @builtin(position) clip_position: vec4,
    @location(0) color: vec4,
};

@vertex
fn vs_main(
    @location(0) inPos: vec3,
    @location(1) color: vec3,
    @location(2) opacity: f32
) -> VertexOutput {
    var out: VertexOutput;
    out.color = vec4(color, opacity);
    out.clip_position = projection * modelView * vec4(inPos, 1.0);
    return out;
}

@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4 {
    return in.color;
}

그리고 렌더링 결과는 다음과 같습니다:

포인트 클라우드 시각화

가우시안 스플랫을 렌더링하는 방법을 이해하려면 3D 가우시안 함수의 기하학적 해석에 익숙해야 합니다. 이를 위해 이 문서를 추천합니다. 자세한 내용은 생략하고 구현에 유용한 내용만 요약하겠습니다.

3D 가우시안은 중심(centroid)과 3x3 공분산 행렬이라는 두 가지 매개변수로 정의됩니다. 직관적으로 중심은 가우시안의 위치이며, 공분산 행렬은 가우시안의 모양(타원체)을 정의합니다.

\mathcal{N}(\mu, \sigma^2)

1D 가우시안을 고려하면, 평균 \mu와 분산 \sigma^2으로 정의됩니다. 이 맥락에서 평균 \mu는 x축에서 가우시안의 중심을 결정하고, \sigma^2은 확산 또는 모양을 결정합니다.

평균과 분산이 다른 1D 가우시안[SOURCE]

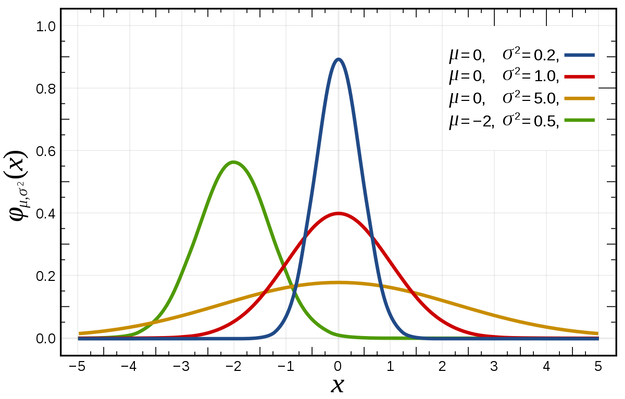
동일한 원리가 2D 및 3D 가우시안으로 확장되며, 이들은 평균 \mu(또는 중심)와 공분산 행렬 \Sigma로 정의됩니다. 2D에서는 공분산 \Sigma가 2x2 행렬이고, 3D에서는 3x3 행렬입니다. 공분산 행렬은 가우시안의 타원체 모양을 정의하는 기하학적 의미를 가집니다.

\mathcal{N}(\mu, \Sigma)

아래는 다양한 2D 가우시안 모양과 해당 공분산 행렬을 보여주는 그림입니다.

2D 가우시안 모양과 공분산[SOURCE]

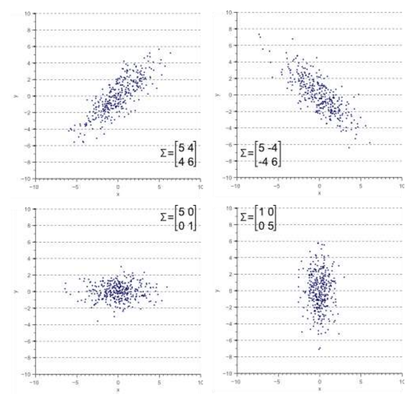
가우시안의 위치를 조정하기 위해 중심(centroid)을 이동할 수 있으며, 공분산 행렬을 회전하고 스케일링하여 모양을 변경할 수도 있습니다. 이 과정은 렌더링 중에 정점에 모델-뷰 행렬을 적용하는 것과 유사하지만, 관련된 수학적 연산은 동일하지 않습니다.

문서에 설명된 기하학적 해석의 근본적인 통찰은 공분산 행렬 \Sigma가 단위 행렬 \mathbf I를 공분산으로 하는 표준 가우시안을 타원체 모양으로 변형시키는 회전 및 스케일링 변환을 지정한다는 것입니다. 이 변환을 3x3 행렬 \textit{T}로 나타내면, 이는 3x3 회전 행렬 \textit{R}과 스케일링 행렬 \textit{S}의 곱으로 분해될 수 있습니다. 따라서:

\begin{aligned} \Sigma &= \textit{T} \textit{I} \textit{T}^\top \\ \Sigma &= \textit{R} \textit{S} (\textit{R} \textit{S})^\top \\ \Sigma &= \textit{R} \textit{S} \textit{S}^\top \textit{R}^\top \\ \end{aligned}

또한, 공분산 행렬에 추가 변환 \textit{V}를 적용하려면 \Sigma^\prime = \textit{V} \Sigma \textit{V}^\top 공식을 사용하여 그렇게 할 수 있습니다. 이는 3D 공분산을 2D 공간으로 투영하는 것과 같은 작업에 중요합니다.

가우시안 스플랫 렌더링을 시작하기 전에, 기준 진실(ground truth)을 설정하는 것이 중요합니다. 그래픽스 프로그램 디버깅은 어려울 수 있으므로, 렌더링 결과를 이 기준 진실과 비교하여 시각화하는 것이 구현의 정확성을 보장하는 데 필수적입니다. 기준 진실을 생성하는 두 가지 주요 방법이 있습니다:

1. 가우시안 분포에서 포인트 클라우드를 생성합니다. 이때 가우시안 값은 샘플 밀도로 사용됩니다.

2. 가우시안의 공분산 행렬에 의해 정의된 동일한 변환을 기반으로 구를 타원체로 변형합니다.

가우시안 스플랫이 렌더링되면, 기준 진실과 겹치는 것을 기대하며, 이는 구현의 정확성에 대한 시각적 확인을 제공합니다.

이 글에서는 첫 번째 방법을 사용할 것입니다. Python은 포인트 샘플링을 훌륭하게 지원하므로, Python에서 가우시안 분포에서 포인트를 샘플링하고 결과를 파일에 저장하는 헬퍼 프로그램을 구현하는 것부터 시작하겠습니다. 그런 다음 WebGPU를 사용하여 이 포인트들을 렌더링할 것입니다.

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import codecs, json 

# Define the parameters of the Gaussian function
mu = [10, 10, 10]
sigma = [[2, 2, 0], [0, 1, 0], [2, 0, 1]]

cov = [[0.46426650881767273, -0.6950497627258301, -0.7515625953674316],
       [ -0.6950497627258301, 2.0874688625335693, 1.7611732482910156],
       [ -0.7515625953674316, 1.7611732482910156, 1.7881864309310913]]



# Generate the data
X = np.random.multivariate_normal(mu, cov, 10000)

json.dump(X.tolist(), codecs.open('points.json', 'w', encoding='utf-8'), 
          separators=(',', ':'), 
          sort_keys=True, 
          indent=4)

코드는 간단합니다. 핵심 줄은 np.random.multivariate_normal(mu, cov, 10000)이며, 이는 다변량 정규 분포(가우시안)에서 10,000개의 포인트를 샘플링합니다. 그런 다음, 이들의 위치를 JSON 파일에 저장합니다.

포인트 클라우드로 시각화된 포인트 샘플

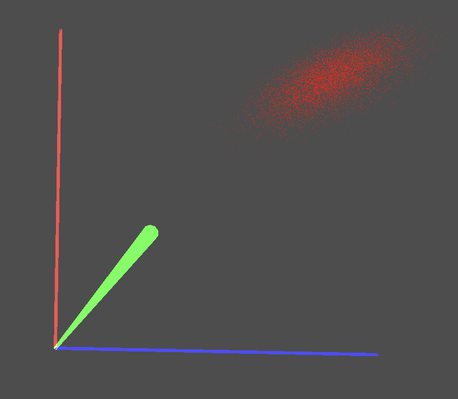
위 프로그램에서 사용된 공분산 행렬은 임의로 보일 수 있습니다. 이 값들이 어떻게 결정되었는지는 이 글의 후반에서 설명할 것입니다.

이제 렌더링하려는 단일 가우시안 스플랫을 정의해봅시다. 특정 가우시안 스플랫이 우리의 목적에 중요하지 않으므로, 임의로 하나를 선택할 것입니다. 이 예시에서는 쿼터니언 (0.601, 0.576, 0.554, 0.01)로 표현된 회전과 (2.0, 0.3, 0.5)의 스케일링 벡터를 선택했습니다. 쿼터니언과 스케일링 벡터는 일반적으로 가우시안 스플랫 파일에 저장되는 정보이기 때문에 사용됩니다.

첫 번째 단계는 회전 행렬과 스케일링 행렬을 도출하여 공분산 행렬을 재구성하는 것입니다. 이 작업을 위해 glMatrix 라이브러리를 사용할 것입니다.

const rot = glMatrix.quat.fromValues(0.601, 0.576, 0.554, 0.01);
let scale = glMatrix.mat4.fromScaling(glMatrix.mat4.create(), glMatrix.vec4.fromValues(2.0, 0.3, 0.5));
scale = glMatrix.mat3.fromMat4(glMatrix.mat3.create(), scale);
const rotation = glMatrix.mat3.fromQuat(glMatrix.mat3.create(), rot);

그런 다음, 방정식 3에 따라 공분산 행렬은 다음과 같이 도출될 수 있습니다:

const T = glMatrix.mat3.multiply(glMatrix.mat3.create(), rotation, scale);

const T_transpose = glMatrix.mat3.transpose(glMatrix.mat3.create(), T);

this.covariance = glMatrix.mat3.multiply(glMatrix.mat3.create(), T, T_transpose);

Python 샘플링 함수에 하드코딩된 공분산 행렬은 여기서 계산된 것과 동일합니다.

렌더링 중에는 카메라를 기반으로 모델-뷰 행렬을 업데이트합니다. 이 모델-뷰 행렬과 투영 행렬을 사용하여, 공분산 행렬을 화면 평면에 정확하게 투영하여 3D 가우시안을 2D 가우시안으로 변환하는 것이 우리의 목표입니다.

첫 번째 단계는 카메라에서 모델-뷰 행렬을 얻고 이를 3x3 행렬(좌상단 3x3 부분)로 변환하는 것입니다. 동차 좌표를 사용한 정점 변환에서, 4x4 행렬은 변환을 위해 구성되며, 오프셋 값은 행렬의 마지막 열에 할당됩니다. 그러나 3x3 공분산 행렬을 다룰 때는 변환을 수행할 수 없으며, 회전 및 스케일링만 가능합니다. 따라서 3x3 모델-뷰 행렬을 얻으려면 단순히 좌상단 3x3 부분을 사용합니다. 이는 회전 및 스케일링을 제거하기 위해 3x3 좌상단 부분에 3x3 단위 행렬이 할당되는 빌보딩(billboarding)과는 대조적입니다.

const W = glMatrix.mat3.transpose(glMatrix.mat3.create(), glMatrix.mat3.fromMat4(glMatrix.mat3.create(), arcballModelViewMatrix));

두 번째 단계는 원근 투영을 수행하는 것입니다. 이는 투영 행렬을 적용하는 것과 유사합니다. 컴퓨터 그래픽스에서 원근 투영을 적용하면 좌표가 카메라 공간 또는 눈 공간에서 클립 공간으로 변환됩니다. 이 변환 전에 가시 공간은 3D 사다리꼴 볼륨인 시야 절두체 내에 포함됩니다. 변환 후 가시 공간은 입방체 볼륨으로 표현됩니다.

투영으로 시야 절두체가 입방체 공간으로 변환[SOURCE]

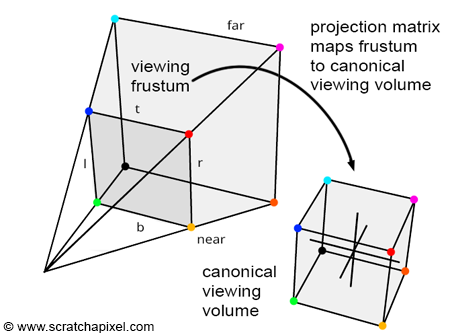
하지만 원근 변환은 아핀(affine) 변환이 아니므로, 원래의 타원체 모양은 투영되면 왜곡될 수 있다는 점에 유의해야 합니다.

원근 투영으로 인한 왜곡[SOURCE]

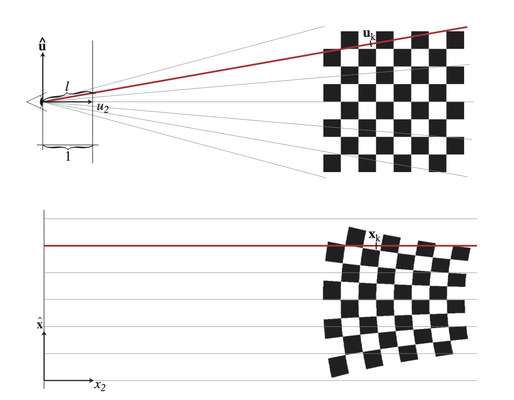
비아핀 변환은 3x3 행렬로 표현될 수 없고 공분산 행렬에 직접 적용될 수 없으므로, 우리의 목표는 투영을 시뮬레이션하는 방식으로 가우시안을 변환할 수 있는 근사치를 찾는 것입니다.

근사 투영의 예시. 왼쪽 하단: 근사 투영은 형태를 왜곡하지 않음. 오른쪽 하단: 원본 투영은 형태를 왜곡함.[SOURCE]

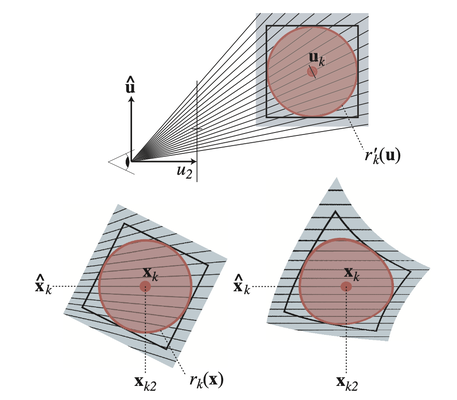
이 변환을 근사화하기 위해, 먼저 점이 화면에 어떻게 투영되는지 고려해봅시다.

한 점의 화면 평면으로의 원근 투영[SOURCE]

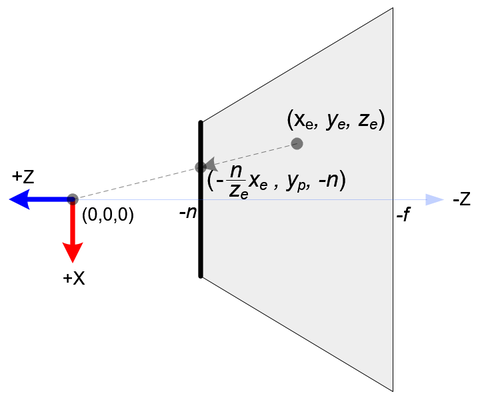
카메라 공간에 있는 점 (x_e, y_e, z_e)가 z=n에서 근접 평면으로 투영될 때, 투영은 다음과 같이 계산할 수 있습니다:

\begin{aligned} x_p &= \frac{-n x_e}{z_e}\\ y_p &= \frac{-n y_e}{z_e}\\ z_p &= - || (x_e, y_e, z_e)^\top ||\\ \end{aligned}

이 (x_e, y_e, z_e)에서 (x_p, y_p, z_p)로의 매핑은 아핀이 아니며 3x3 행렬로 표현될 수 없습니다. 여기 참조된 논문에 따르면, 이 변환을 매핑 함수의 테일러 전개(Taylor expansion)의 첫 두 항인 v_p + J(v-v_c)를 사용하여 근사화할 수 있습니다. 여기서 v_p는 가우시안의 투영된 중심(centroid)이고, J는 야코비(Jacobian) 또는 1차 미분입니다.

테일러 전개의 개념은 이름이 어렵게 들릴 수 있지만 실제로는 아주 간단합니다. 1D 미지 함수 y = f(x)를 사용하여 설명해봅시다. 우리의 목표는 특정 입력 점 x_0 근처에서 함수를 추정하는 것입니다. x_0 주변의 아주 작은 구간에 초점을 맞추면, 함수는 직선으로 근사될 수 있습니다. 이 직선은 함수 f의 미분을 계산하여 얻을 수 있습니다. 따라서 x가 x_0에 가까울 때의 f(x) 값은 \bar{y} = f(x_0) + f^\prime(x_0)(x - x_0)로 근사될 수 있습니다.

우리의 투영 시나리오에서, f(x_0)는 가우시안 중심(centroid)의 투영된 위치를 나타내며, 이는 모델-뷰 행렬과 중심 위치를 사용하여 쉽게 계산할 수 있습니다. f^\prime(x_0)는 야코비 행렬에 해당하며, 우리는 이를 사용하여 공분산 행렬을 변환할 것입니다.

야코비 행렬(전치)은 다음과 같이 계산할 수 있습니다:

\begin{pmatrix} \frac{d x_p}{d x_e} & \frac{d y_p}{d x_e} & \frac{d z_p}{d x_e}\\ \frac{d x_p}{d y_e} & \frac{d y_p}{d y_e} & \frac{d z_p}{d y_e}\\ \frac{d x_p}{d z_e} & \frac{d y_p}{d z_e} & \frac{d z_p}{d z_e}\\ \end{pmatrix}

방정식 4에 따라 야코비 행렬은 다음과 같이 계산할 수 있습니다:

\begin{pmatrix} -\frac{n}{z_e} & 0 & 0\\ 0 & -\frac{n}{z_e} & 0\\ \frac{x_e}{z_e^2} & \frac{y_e}{z_e^2} & 0\\ \end{pmatrix}

마지막 열이 모두 0이어서는 안 되지만, 우리의 참조 코드에서는 마지막 열이 실제로 0으로 설정되어 있습니다. 이 이유는 가우시안 투영의 경우, z_p가 상수라고 가정함으로써 깊이 정보를 효과적으로 제거할 수 있기 때문이라고 생각합니다. 이는 가우시안에 대해 깊이 테스트가 필요 없으며, 대신 앞에서 뒤로 정렬하여 그 순서대로 렌더링하기 때문입니다.

여기 코드로 야코비 행렬(열 우선 순서)이 계산되는 방식이 있습니다. 이는 원근 투영 행렬을 기반으로 합니다:

const focal = {
    x: projectionMatrix[0] * devicePixelRatio * renderDimension.x * 0.5,
    y: projectionMatrix[5] * devicePixelRatio * renderDimension.y * 0.5
}

const viewCenter = glMatrix.vec4.transformMat4(glMatrix.vec4.create(), glMatrix.vec4.fromValues(10, 10, 10, 1.0), arcballModelViewMatrix);

const s = 1.0 / (viewCenter[2] * viewCenter[2]);

const J = glMatrix.mat3.fromValues(
    -focal.x / viewCenter[2], 0., (focal.x * viewCenter[0]) * s,
    0., -focal.y / viewCenter[2], (focal.y * viewCenter[1]) * s,
    0., 0., 0.
);

초점 벡터는 투영 행렬에서 첫 번째와 여섯 번째 요소를 추출하여 계산할 수 있습니다. 이 요소들은 수평 및 수직 시야각의 절반의 아크탄젠트를 나타냅니다. 이들을 캔버스의 절반 너비와 절반 높이로 각각 곱하면, 카메라에서 근접 평면까지의 거리를 얻을 수 있습니다. 이론적으로 focal.x와 focal.y는 동일해야 합니다.

3x3 모델-뷰 행렬 W와 야코비 행렬 J를 모두 사용하여 이제 다음과 같이 공분산을 업데이트할 수 있습니다:

const W = glMatrix.mat3.transpose(glMatrix.mat3.create(), glMatrix.mat3.fromMat4(glMatrix.mat3.create(), arcballModelViewMatrix));
const T = glMatrix.mat3.multiply(glMatrix.mat3.create(), W, J);

let new_c = glMatrix.mat3.multiply(glMatrix.mat3.create(), glMatrix.mat3.transpose(glMatrix.mat3.create(), T), glMatrix.mat3.multiply(glMatrix.mat3.create(), this.covariance, T));

업데이트된 공분산으로, 우리는 그것의 2x2 좌상단 코너를 추출합니다. 이는 투영된 2D 가우시안의 공분산을 나타냅니다. 다음으로, 2D 가우시안에서 두 개의 기본 벡터를 복구해야 하는데, 이는 상위 두 고유값의 고유 벡터에 해당합니다.

이는 다음 공식을 사용하여 계산됩니다:

const cov2Dv = glMatrix.vec3.fromValues(new_c[0], new_c[1], new_c[4]);

let a = cov2Dv[0];
let b = cov2Dv[1];
let d = cov2Dv[2];

let D = a * d - b * b;
let trace = a + d;
let traceOver2 = 0.5 * trace;
let term2 = Math.sqrt(trace * trace / 4.0 - D);
let eigenValue1 = traceOver2 + term2;
let eigenValue2 = Math.max(traceOver2 - term2, 0.00); // prevent negative eigen value

const maxSplatSize = 1024.0;
let eigenVector1 = glMatrix.vec2.normalize(glMatrix.vec2.create(), glMatrix.vec2.fromValues(b, eigenValue1 - a));
// since the eigen vectors are orthogonal, we derive the second one from the first
let eigenVector2 = glMatrix.vec2.fromValues(eigenVector1[1], -eigenVector1[0]);

let basisVector1 = glMatrix.vec2.scale(glMatrix.vec2.create(), eigenVector1, Math.min(Math.sqrt(eigenValue1) * 4, maxSplatSize));
let basisVector2 = glMatrix.vec2.scale(glMatrix.vec2.create(), eigenVector2, Math.min(Math.sqrt(eigenValue2) * 4, maxSplatSize));

정점 셰이더 코드에서는 기준 벡터를 활용하여 화면 정렬 쿼드를 구성합니다. 쿼드의 긴 변은 첫 번째 기준 벡터와 평행해야 하며, 짧은 변은 두 번째 고유 벡터와 평행해야 합니다.

var clipCenter:vec4 = projection * modelView * pos;

var ndcCenter:vec3 = clipCenter.xyz / clipCenter.w;

var ndcOffset:vec2 = vec2(inPos.x * basisVector1 + inPos.y * basisVector2) * basisViewport;

out.clip_position = vec4(ndcCenter.xy + ndcOffset, ndcCenter.z, 1.0);

셰이더 코드에서는 NDC(정규화된 장치 좌표)에서 중심(centroid)의 위치를 수동으로 계산합니다. NDC는 x축과 y축 모두에 대해 [-1, 1] 범위를 가지므로, ndcOffset을 스케일링해야 합니다. 야코비가 픽셀을 단위 길이로 사용하여 계산되었기 때문에, w와 h가 각각 캔버스의 너비와 높이인 (\frac{w}{2},\frac{h}{2})로 스케일 다운해야 합니다.

기준 진실 포인트 클라우드와 겹치는 가우시안 렌더링 결과

렌더링 결과는 위에 나와 있습니다. 보시다시피 가우시안이 올바르게 렌더링되었고, 기준 진실 포인트 클라우드와 완벽하게 겹쳐집니다.

이제 단일 가우시안 스플랫을 렌더링했으니, 전체 포인트 클라우드를 렌더링하도록 프로그램을 확장해야 합니다. 가우시안 스플랫은 반투명하기 때문에 블렌딩을 활성화하고 앞에서 뒤로 순서대로 렌더링해야 합니다.

여기서 우리의 이전 기수 정렬(radix sort) 알고리즘이 등장합니다. 과정은 다음과 같습니다: 먼저, 각 스플랫에 대한 투영된 기본(basis)과 카메라까지의 거리를 계산합니다. 이 과정은 이전에 설명한 것과 동일하지만, 이를 컴퓨트 셰이더에서 구현하고 모든 스플랫에 한 번에 적용할 것입니다. 그런 다음, GPU 기수 정렬을 사용하여 스플랫을 앞에서 뒤로 재정렬합니다. 마지막으로, 정렬된 가우시안 스플랫을 반복하여 순서대로 렌더링합니다.

이제 카메라에서 스플랫까지의 거리를 효율적으로 계산하는 방법을 살펴보겠습니다:

// given centroids, covariance, modelView, projection;
// compute 2d basis, distance
@binding(0) @group(0) var centroid :array>;
@binding(1) @group(0) var covariance: array>;
@binding(2) @group(0) var basis: array>;
@binding(3) @group(0) var distance: array;
@binding(4) @group(0) var id: array;
@binding(5) @group(0) var splatCount: u32;
@binding(6) @group(0) var readback: array>;

@binding(0) @group(1) var modelView: mat4x4;
@binding(1) @group(1) var projection: mat4x4;
@binding(2) @group(1) var screen: vec2;

@compute @workgroup_size(256)
fn main(@builtin(global_invocation_id) GlobalInvocationID : vec3,
  @builtin(local_invocation_id) LocalInvocationID: vec3,
  @builtin(workgroup_id) WorkgroupID: vec3) {
    var gid = GlobalInvocationID.x;

    if (gid < splatCount) {
        var covarianceFirst = covariance[gid*2];
        var covarianceSecond = covariance[gid*2+1];

        var covarianceMatrix: mat3x3 = mat3x3(
            covarianceFirst.x,
            covarianceFirst.y,
            covarianceFirst.z,
            covarianceFirst.y,
            covarianceSecond.x,
            covarianceSecond.y,
            covarianceFirst.z,
            covarianceSecond.y,
            covarianceSecond.z);

        var modelView3x3:mat3x3 = transpose( mat3x3(modelView[0].xyz, modelView[1].xyz, modelView[2].xyz));

        var cameraFocalLengthX:f32 = projection[0][0] *
        screen.x * 0.5;
        var cameraFocalLengthY:f32 = projection[1][1] *
        screen.y * 0.5;

        var center:vec4 = vec4(centroid[gid], 1.0);

        var viewCenter:vec4 =   modelView * center;
        var s:f32 = 1.0 / (viewCenter.z * viewCenter.z);

        var J = mat3x3(
            cameraFocalLengthX / viewCenter.z, 0.0, -(cameraFocalLengthX * viewCenter.x) * s,
            0.0, cameraFocalLengthY / viewCenter.z, -(cameraFocalLengthY * viewCenter.y) * s,
            0.0, 0.0, 0.0
        );

        var T:mat3x3 =  modelView3x3 * J ;

        var T_t:mat3x3 = transpose(T);
    
        var new_c:mat3x3 =  T_t * covarianceMatrix * T;
        
        var cov2Dv:vec3 = vec3(new_c[0][0] , new_c[0][1], new_c[1][1]);
          
        var a:f32 = cov2Dv.x;
        var b:f32 = cov2Dv.y;
        var d:f32 = cov2Dv.z;

        var D:f32 = a * d - b * b;
        var trace:f32 = a + d;
        var traceOver2:f32 = 0.5 * trace;
        var term2:f32 = sqrt(trace * trace / 4.0 - D);
            
        var eigenValue1:f32 = traceOver2 + term2;
        var eigenValue2:f32 = max(traceOver2 - term2, 0.0);

        const maxSplatSize:f32 = 1024.0;
        var eigenVector1:vec2 = normalize(vec2(b, eigenValue1 - a));
        var eigenVector2:vec2 = vec2(eigenVector1.y, -eigenVector1.x);
  
        var basisVector1:vec2 = eigenVector1 * min(sqrt(eigenValue1)*4, maxSplatSize);
        var basisVector2:vec2 = eigenVector2 * min(sqrt(eigenValue2)*4, maxSplatSize);
        readback[gid] = vec4(basisVector1,basisVector2);
        var dis:vec4 = projection * modelView * center;
        distance[gid] = u32(((dis.z / dis.w+1.0)*0.5) * f32(0xFFFFFFFF >> 8));     
        basis[gid] = vec4(basisVector1, basisVector2);
    } else {
        distance[gid] = 0xFFFFFFFF;
    }
    id[gid] = gid;
}

대부분의 코드는 이전에 설명되었습니다. 여기서 다른 점은 스플랫과 카메라 사이의 거리 계산도 통합했다는 것입니다. 계산 자체는 투영 행렬을 적용하는 것과 동일합니다.

여기서 주의해야 할 몇 가지 중요한 세부 사항이 있습니다. 첫째, 거리 값을 스케일링하고 정수로 변환합니다: distance[gid] = u32(dis.z / dis.w * f32(0xFFFFFFFF >> 8));. 이 이유는 우리의 기수 정렬이 정수만 처리할 수 있기 때문입니다. 둘째, 패딩 스플랫의 경우, 거리를 가능한 최대 값으로 설정합니다: distance[gid] = 0xFFFFFFFF;. 스플랫의 수가 항상 512의 배수라고 보장할 수 없습니다. 따라서 일반적으로 입력 배열의 끝에 패딩을 해야 합니다. 이 패딩된 더미 스플랫의 경우, 정렬 후 배열의 끝에 위치하여 쉽게 잘라낼 수 있도록 가능한 최대 거리를 부여합니다.

다음은 정렬 부분입니다. 이전에 본 것과 거의 동일합니다. 차이점은 셔플링 부분에 있습니다. 배열이 더 복잡하기 때문에 단일 정수보다 더 많은 데이터를 이동해야 합니다. 그러나 원칙은 동일합니다.

마지막으로, 스플랫이 정렬되면 앞에서 뒤로 렌더링을 적용합니다:

encode(encoder) {
    encoder.setPipeline(this.splatPipeline);
    encoder.setBindGroup(0, this.splatUniformBindGroup0);
    encoder.setBindGroup(1, this.splatUniformBindGroup1)
    encoder.setVertexBuffer(0, this.splatPositionBuffer);
    encoder.setVertexBuffer(1, this.idBuffer);
    for (let i = this.actualSplatSize - 1; i >= 0; --i) {
        encoder.draw(4, 1, 0, i);
    }
}

왜 for 루프 대신 인스턴스 렌더링(instanced rendering) 기법을 사용할 수 없는지 궁금할 수 있습니다. 그 이유는 정확한 블렌딩을 보장하기 위해 렌더링 순서를 유지해야 하기 때문입니다. 인스턴스 렌더링을 사용하면 스플랫이 병렬로 그려지기 때문에 렌더링 순서가 보장되지 않습니다.

렌더링된 가우시안 스플래팅 장면