1.16 조명
이 섹션에서는 컴퓨터 그래픽스에서 가장 기본적인 조명 알고리즘을 살펴보겠습니다. 카메라와 마찬가지로, GPU 파이프라인 내에는 조명에 대한 직접적인 개념이 없다는 점에 유의해야 합니다. 조명 계산의 책임은 우리, 즉 개발자에게 있습니다. 조명은 컴퓨터 그래픽스에서 가장 오래되고 광범위하게 연구된 주제 중 하나이며, 지속적인 개발을 통해 그 가능성의 경계를 계속해서 넓혀가고 있습니다.
모든 조명 솔루션은 이미지 품질과 렌더링 속도 사이의 미묘한 균형을 포함합니다. 역사적으로 렌더링 방법은 오프라인과 실시간이라는 두 가지 범주로 나뉘었습니다. 오프라인 렌더링은 가능한 최고의 이미지 품질을 목표로 했으며, 대규모 컴퓨터 클러스터를 사용하여 렌더링에 상당한 시간이 소요될 수 있는 영화 제작에 자주 사용되었습니다. 반면, 실시간 조명은 렌더링의 반응성을 우선시하면서 일부 시각적 품질을 희생했습니다. 이 접근 방식은 게임 및 대화형 애플리케이션의 핵심이었습니다.
최근 몇 년 동안 GPU의 성능이 향상되면서 이 두 범주 간의 경계가 모호해졌습니다. 비디오 게임은 한때 영화 산업의 전유물이었던 기술을 채택하여 영화 같고 매우 사실적으로 발전했습니다.
이 튜토리얼에서는 퐁 셰이딩(Phong shading)으로 알려진 간단하면서도 성능이 뛰어난 조명 방식을 구현할 것입니다. 이 기술은 가장 널리 사용되는 조명 솔루션이 되어 많은 애플리케이션의 기본 선택이 되었습니다. 이 튜토리얼을 정점별 조명(per-vertex lighting)과 프래그먼트별 조명(per-fragment lighting)의 두 부분으로 나누어 설명하겠습니다.
정점별 조명은 각 정점에서 조명 효과를 계산하고, 삼각형 전체 표면에 대한 효과를 시뮬레이션하기 위해 결과 색상을 보간합니다. 이 접근 방식은 정점에서 조명을 드문드문 계산하기 때문에 매우 효율적입니다. 그러나 낮은 폴리곤 수의 모델에서는 덜 정확한 결과를 생성할 수 있습니다.
두 번째 솔루션인 프래그먼트별 조명은 다른 접근 방식을 취합니다. 정점에서만 조명을 계산하는 대신, 정점 노멀을 보간하고 프래그먼트 셰이더 단계에서 조명을 계산합니다. 이 방법은 더 정확한 조명 계산에 중요한 더 부드러운 표면으로 더 나은 결과를 제공합니다. 단점은 정점별 조명보다 더 많은 계산 능력이 필요하다는 것입니다.
퐁 셰이딩(Phong Shading) 이론
부이 투옹 퐁(Bui Tuong Phong)이 개발한 퐁 반사 모델은 실시간 성능을 유지하면서 광범위한 조명 효과를 시뮬레이션하도록 설계되었습니다. 이 모델은 시각적 품질과 계산 효율성의 균형 덕분에 컴퓨터 그래픽스에서 중요한 기반이 되었습니다.
핵심적으로, 퐁 조명 모델은 빛 상호작용을 앰비언트(ambient), 디퓨즈(diffuse), 스페큘러(specular)의 세 가지 고유한 구성 요소로 나눕니다.
앰비언트 구성 요소는 환경 조명을 시뮬레이션하여 표면의 방향에 관계없이 모든 표면을 균일하게 비추는 기준 빛을 제공합니다. 이는 광원에 의해 직접 조명되지 않는 영역에서 개체가 비정상적으로 어둡게 보이는 것을 방지합니다.
디퓨즈 구성 요소는 거칠고 무광택 표면과의 빛 상호작용을 재현합니다. 이는 들어오는 빛의 방향과 표면 노멀을 사용하여 계산되며, 고르지 않은 표면에서 빛이 어떻게 산란되는지를 시뮬레이션합니다. 이 구성 요소는 시점 독립적이므로 보는 사람의 위치에 관계없이 동일하게 나타납니다.
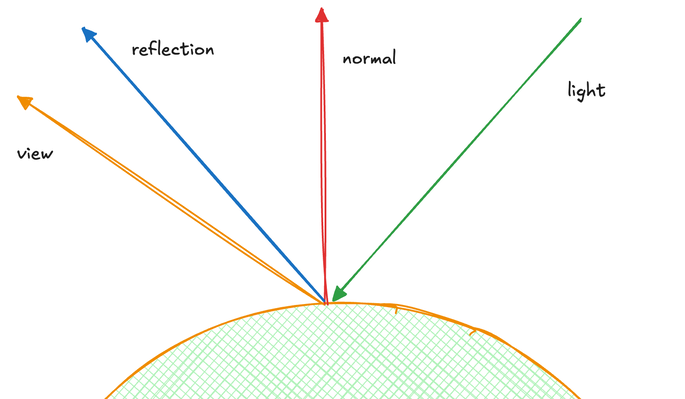
스페큘러 구성 요소는 반사 표면에서의 빛의 동작을 모델링합니다. 그 강도는 반사 방향과 시야 방향 간의 관계에 따라 결정됩니다. 이는 표면에 하이라이트 지점을 생성하며, 강도는 광택(shininess) 값으로 제어됩니다. 디퓨즈 구성 요소와 달리 스페큘러 조명은 보는 사람의 각도에 따라 크게 달라지며, 보는 위치의 작은 변화도 스페큘러 하이라이트에 상당한 변화를 일으킬 수 있습니다.
퐁 셰이딩 방정식은 다음과 같이 요약할 수 있습니다:
I = k_a*i_a + k_d * (L \dot N) * i_d + k_s * (R \dot V)^\alpha
이 방정식에서:
k_a,k_d, 및k_s는 각각 앰비언트, 디퓨즈, 스페큘러 구성 요소의 가중치입니다.i_a는 일정한 앰비언트 빛을 나타냅니다.i_d는 디퓨즈 빛 상수입니다.L은 빛의 방향 벡터입니다.N은 표면 노멀 벡터입니다.R은 반사 방향 벡터입니다.V는 시야 방향 벡터입니다.\alpha는 재질의 반사율을 결정하는 광택 계수입니다. 값이 높을수록 작고 집중적인 스페큘러 하이라이트가 발생하여 더 부드럽고 거울과 같은 표면을 시뮬레이션합니다. 값이 낮을수록 더 넓은 스페큘러 영역이 생성되어 더 거칠고 분산된 재질을 근사합니다.
정점별 조명(Per-vertex lighting)
이 튜토리얼에서는 단일 광원을 지원하도록 조명 방정식을 단순화할 것입니다. 완전한 퐁 셰이딩 모델에서는 일반적으로 각 광원의 기여를 합산하여 여러 광원을 처리합니다. 이 단순화를 통해 복잡성에 압도되지 않고 핵심 개념에 집중할 수 있습니다.
플레이그라운드 실행 - 1_16_1_lighting주요 셰이더 변경 사항을 살펴보겠습니다:
@group(0) @binding(3)
var lightDirection: vec3;
@group(0) @binding(4)
var viewDirection: vec3;
두 가지 새로운 유니폼 변수: lightDirection과 viewDirection을 도입합니다. 단순화를 위해 광원은 카메라와 같은 위치에 있다고 가정하여 이 방향들이 동일하도록 합니다. 더 복잡한 시나리오에서는 이들이 종종 다를 수 있습니다.
const ambientColor:vec4 = vec4(0.15, 0.0, 0.0, 1.0);
const diffuseColor:vec4 = vec4(0.25, 0.25, 0.25, 1.0);
const specularColor:vec4 = vec4(1.0, 1.0, 1.0, 1.0);
const shininess:f32 = 20.0;
새로운 유니폼에 이어 재질 속성에 대한 상수를 정의합니다. ambientColor, diffuseColor, specularColor는 빛에 대한 재질의 반응을 나타냅니다. shininess 값은 스페큘러 하이라이트의 크기와 강도를 제어하며, 값이 높을수록 작고 집중적인 하이라이트가 생성됩니다.
const diffuseConstant:f32 = 1.0;
const specularConstant:f32 = 1.0;
const ambientConstant: f32 = 1.0;
또한 diffuseConstant, specularConstant, ambientConstant의 세 가지 상수를 정의합니다. 이 상수들을 통해 각 조명 구성 요소의 강도를 조절할 수 있습니다. 현재 1.0으로 설정되어 있으며, 조명 효과를 미세 조정하기 위해 수정할 수 있습니다.
코드를 모듈화하고 가독성을 높이기 위해 스페큘러 및 디퓨즈 조명 계산을 캡슐화하는 두 가지 함수를 생성합니다. 스페큘러 조명 함수를 살펴보겠습니다:
스페큘러 구성 요소는 다음 방정식을 사용하여 계산됩니다:
S = (R \dot V)^\alpha
여기서:
R은 반사 방향
V는 시야 방향
\alpha는 광택 계수
이 방정식은 다음 함수에 구현되어 있습니다:
fn specular(lightDir:vec3, viewDir:vec3, normal:vec3, specularColor:vec3,
shininess:f32) -> vec3 {
var reflectDir:vec3 = reflect(-lightDir, normal);
var specDot:f32 = max(dot(reflectDir, viewDir), 0.0);
return pow(specDot, shininess) * specularColor;
}
스페큘러 함수는 퐁 조명 모델의 스페큘러 구성 요소를 계산합니다. 빛의 방향, 시야 방향, 표면 노멀, 스페큘러 색상 및 광택을 고려합니다. 이 함수는 WebGPU의 내장 reflect() 함수를 사용하여 반사 방향을 먼저 계산하며, 이는 우리 코드를 단순화합니다. 그런 다음, 반사 방향과 시야 방향의 내적을 취하여 반사의 강도를 계산하고, 음수 값이 나오지 않도록 0.0으로 클램프합니다. 마지막으로, 광택 계수를 적용하여 스페큘러 하이라이트의 크기와 강도를 제어합니다.
fn diffuse(lightDir:vec3, normal:vec3, diffuseColor:vec3) -> vec3{
return max(dot(lightDir, normal), 0.0) * diffuseColor;
}
디퓨즈 함수는 퐁 모델의 디퓨즈 구성 요소를 다음 방정식에 따라 구현합니다:
D = (L \dot N) * i_d
여기서 L은 빛의 방향, N은 표면 노멀, i_d는 디퓨즈 색상입니다. L과 N의 내적은 빛이 표면에 얼마나 직접적으로 닿는지 결정하며, max 함수는 음수 조명 값을 얻지 않도록 합니다.
@vertex
fn vs_main(
@location(0) inPos: vec3,
@location(1) inNormal: vec3
) -> VertexOutput {
var n:vec3 = normalize((normalMatrix * vec4(inNormal, 0.0)).xyz);
var viewDir:vec3 = normalize((normalMatrix * vec4(-viewDirection, 0.0)).xyz);
var lightDir:vec3 = normalize((normalMatrix * vec4(-lightDirection, 0.0)).xyz);
var radiance:vec3 = ambientColor.rgb * ambientConstant +
diffuse(lightDir, n, diffuseColor.rgb)* diffuseConstant +
specular(lightDir, viewDir, n, specularColor.rgb, shininess) * specularConstant;
var out: VertexOutput;
out.clip_position = projection * modelView * vec4(inPos, 1.0);
out.color = radiance;
return out;
}
정점 셰이더 vs_main에서는 여러 가지 중요한 단계를 수행합니다:
우리는 normalMatrix를 사용하여 표면 노멀, 시야 방향 및 빛의 방향을 변환합니다. 이 행렬은 모델 및 뷰 변환을 모두 포함하여 모든 벡터가 동일한 좌표 공간에 있도록 보장합니다. 그런 다음 정확한 조명 계산을 위해 이 벡터들을 정규화합니다.
복사본 계산은 앰비언트, 디퓨즈 및 스페큘러 구성 요소를 결합합니다. 각 구성 요소는 각 상수에 곱해져 조명 효과를 미세 조정할 수 있습니다.
마지막으로, 클립 위치(투영 및 모델뷰 행렬에 의해 변환됨)와 계산된 복사본 색상을 포함하여 정점 출력을 설정합니다.
여기서 이러한 계산을 카메라 공간에서 수행하지만, 세계 좌표계에서 조명을 계산하는 것도 유효합니다.
let lightDirectionBuffer = new Float32Array([-1.0, -1.0, -1.0]);
const lightDirectionUniformBuffer = createGPUBuffer(device, lightDirectionBuffer, GPUBufferUsage.UNIFORM);
const viewDirectionUniformBuffer = createGPUBuffer(device, new Float32Array([-1.0, -1.0, -1.0]), GPUBufferUsage.UNIFORM);
JavaScript 코드에서는 두 개의 새로운 유니폼 버퍼인 lightDirectionUniformBuffer와 viewDirectionUniformBuffer를 도입합니다. 이 버퍼들은 각각 광원과 카메라 시야의 방향 벡터를 저장합니다.
두 방향 모두 (-1.0, -1.0, -1.0)으로 초기화합니다. 이 선택은 광원과 카메라가 모두 월드 공간의 (3, 3, 3) 위치에 있고 원점을 향하고 있다고 가정합니다. 음수 값은 이 위치에서 우리 장면의 중앙을 향하는 방향을 나타냅니다. 더 복잡한 장면에서는 이러한 방향이 다를 수 있고, 카메라 움직임이나 광원 위치 변경에 따라 동적으로 업데이트될 수 있다는 점에 유의하는 것이 중요합니다.
let uniformBindGroupLayout = device.createBindGroupLayout({
entries: [
{
binding: 0,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 1,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 2,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 3,
visibility: GPUShaderStage.VERTEX,
buffer: {}
},
{
binding: 4,
visibility: GPUShaderStage.VERTEX,
buffer: {}
}
]
});
let uniformBindGroup = device.createBindGroup({
layout: uniformBindGroupLayout,
entries: [
{
binding: 0,
resource: {
buffer: modelViewMatrixUniformBuffer
}
},
{
binding: 1,
resource: {
buffer: projectionMatrixUniformBuffer
}
},
{
binding: 2,
resource: {
buffer: normalMatrixUniformBuffer
}
},
{
binding: 3,
resource: {
buffer: lightDirectionUniformBuffer
}
},
{
binding: 4,
resource: {
buffer: viewDirectionUniformBuffer
}
}
]
});
이 새로운 유니폼을 렌더링 파이프라인에 통합하기 위해 GPU 바인딩 구성을 업데이트해야 합니다. 마찬가지로, uniformBindGroup에서는 이 바인딩들을 새로 생성된 유니폼 버퍼에 연결하는 해당 엔트리를 생성합니다.
프래그먼트별 조명(Per-fragment lighting)
이제 정점별 셰이딩에서 프래그먼트별 셰이딩으로의 전환을 살펴보겠습니다. 이 기술은 렌더링된 장면의 시각적 품질을 크게 향상시킵니다.
플레이그라운드 실행 - 1_16_2_lighting이전의 정점별 접근 방식에서는 각 정점에서 조명 효과를 계산한 다음 이 결과를 삼각형 표면에 걸쳐 보간했습니다. 이 방법은 계산 효율적이지만, 특히 낮은 폴리곤 모델로 표현된 곡면에서는 눈에 띄는 평탄화 아티팩트를 발생시켰습니다.
프래그먼트별 셰이딩은 다른 접근 방식을 취합니다. 정점에서 최종 조명을 계산하는 대신, 시야 방향, 빛 방향 및 표면 노멀을 프래그먼트 셰이더 단계로 전달합니다. 최종 색상을 보간하는 대신, 표면 노멀만 삼각형에 걸쳐 보간합니다. 그런 다음, 보간된 노멀을 사용하여 각 프래그먼트에 대해 조명 계산을 수행합니다.
이 방법은 곡률의 표현을 향상시킵니다. 삼각형은 본질적으로 평평하지만, 종종 곡면을 근사합니다. 정점별 조명은 모든 삼각형을 실제로 평평하게 처리하여 곡률의 환상을 잃게 만듭니다. 프래그먼트 셰이딩은 노멀을 보간함으로써 부드러운 곡면의 모양을 더 잘 유지합니다.
이 방법이 더 정확한 근사치를 제공하지만 여전히 근사치라는 점을 이해하는 것이 중요합니다. 보간된 노멀은 모든 지점에서 표면의 실제 노멀이 아니지만, 정점별 조명의 평평한 셰이딩에 비해 상당한 개선을 제공합니다.
이 기술은 각 정점 대신 각 프래그먼트에 대해 조명 계산을 수행하므로 성능 비용이 발생합니다. 그러나 시각적 개선은 특히 최신 하드웨어에서는 추가 계산 비용을 감수할 가치가 있는 경우가 많습니다.
다음 섹션에서는 프래그먼트별 셰이딩의 구현 세부 사항을 자세히 살펴보겠습니다.
@vertex
fn vs_main(
@location(0) inPos: vec3,
@location(1) inNormal: vec3
) -> VertexOutput {
var out: VertexOutput;
out.viewDir = normalize((normalMatrix * vec4(-viewDirection, 0.0)).xyz);
out.lightDir = normalize((normalMatrix * vec4(-lightDirection, 0.0)).xyz);
out.normal = normalize(normalMatrix * vec4(inNormal, 0.0)).xyz;
out.clip_position = projection * modelView * vec4(inPos, 1.0);
return out;
}
프래그먼트별 셰이딩으로의 전환을 용이하게 하는 셰이더 코드 변경 사항을 살펴보겠습니다. 각 조명 채널을 계산하는 동일한 논리를 유지하지만, 정점 셰이더는 이제 다른 목적을 수행합니다. 정점 수준에서 최종 조명을 계산하는 대신, 시야 방향과 빛 방향을 프래그먼트 셰이더로 전달하는 데 중점을 둡니다.
@fragment
fn fs_main(in: VertexOutput) -> @location(0) vec4 {
var lightDir:vec3 = in.lightDir;
var n:vec3 = normalize(in.normal);
var viewDir: vec3 = in.viewDir;
var radiance:vec3 = ambientColor.rgb * ambientConstant +
diffuse(lightDir, n, diffuseColor.rgb)* diffuseConstant +
specular(lightDir, viewDir, n, specularColor.rgb, shininess) * specularConstant;
return vec4(radiance ,1.0);
}
프래그먼트 셰이더 단계에서는 보간된 노멀을 정규화하는 것이 중요합니다. 보간은 이 노멀의 길이에 영향을 줄 수 있으며, 정확한 조명 계산을 위해서는 정규화되어야 합니다. 그러나 빛과 시야 방향의 값은 모든 정점에서 일관되므로 이들에 대한 정규화는 필요하지 않습니다.
정규화된 노멀과 안정적인 빛 및 시야 방향을 사용하여 프래그먼트 셰이더에서 복사본을 계산하고, 이는 출력 색상으로 사용됩니다.

프래그먼트별 조명을 사용하면 표면의 부드러움이 크게 향상되는 것을 확인할 수 있습니다.