1.15 노멀 이해하기

이 튜토리얼에서는 컴퓨터 그래픽스의 모든 측면에서 중요한 요소인 노멀 개념을 살펴보겠습니다. 노멀은 조명 계산에 광범위하게 사용됩니다. 컴퓨터 그래픽스에서 조명 효과는 빛이 표면의 재료와 어떻게 상호작용하는지에 따라 달라집니다. 빛이 표면을 비추는 방향은 표면의 모양을 크게 바꿀 수 있으므로, 표면이 어느 방향을 향하는지 결정하는 것이 중요합니다. 이 방향적 측면을 노멀 방향이라고 합니다.

2D로 시각화된 평면 노멀과 부드러운 노멀

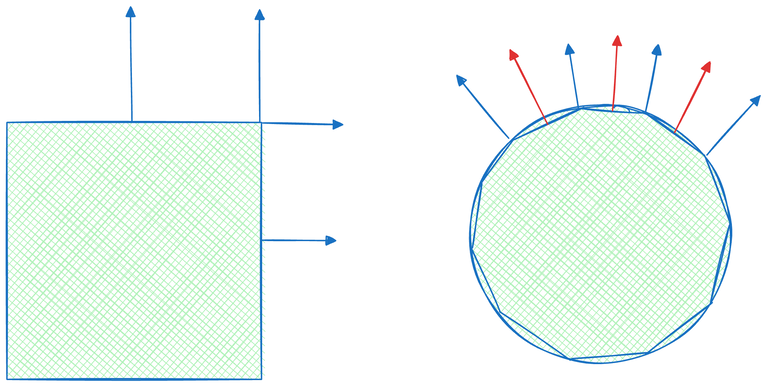
표면의 향하는 방향이라는 개념은 단순화된 설명입니다. 실제로는 노멀이 표면에서 어떻게 변하고 어디에 정의되어야 하는지는 애플리케이션에 따라 달라질 수 있습니다. 가장 간단한 시나리오에서는 날카로운 주름이나 특징을 가진 평면 표면을 렌더링할 때 각 면에 하나의 노멀을 부착하여 이러한 특징에서 노멀이 갑자기 변하도록 할 수 있습니다. 여러 면을 연결하는 가장자리나 정점은 인접한 각 면에 대해 하나의 노멀을 가지므로 표면 매끄러움의 불연속성을 반영합니다.

정점 노멀은 삼각형에서 보간되어 부드러운 노멀 전환을 생성할 수 있습니다

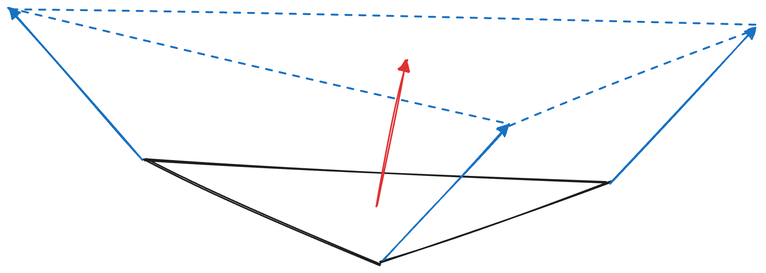
다른 시나리오에서는 노멀이 갑자기 변하지 않는 부드러운 표면을 선호할 수 있습니다. 이 경우 노멀은 대신 정점에 정의될 수 있으며, 이는 근처 표면 노멀의 평균으로 정의됩니다. 이렇게 정점 정의된 노멀은 래스터화 단계에서 보간되어 삼각형 전체에 걸쳐 부드러운 노멀 전환을 생성하고 더 부드러운 렌더링을 가능하게 합니다.

거친 벽이나 주름진 표면과 같은 미세 구조를 모델링하는 더 복잡한 경우에는 면별 노멀과 정점별 노멀 모두 충분한 해상도를 제공하지 못할 수 있습니다. 이러한 상황에서는 노멀을 텍스처 맵에 저장하여 단일 삼각형이 텍스처에서 샘플링된 수많은 노멀을 가질 수 있도록 할 수 있습니다.

노멀은 기하학적 형상에 기반하여 계산되거나 파일에서 로드될 수 있습니다. 대부분의 3D 모델 파일에는 정점 위치뿐만 아니라 노멀도 포함되어 있습니다. 이 튜토리얼에서는 노멀을 포함하도록 로딩 로직을 확장합니다.

for (let f of obj.result.models[0].faces) {
    let points = [];
    let facet_indices = [];
    for (let v of f.vertices) {
        const index = v.vertexIndex - 1;
        indices.push(index);

        const vertex = glMatrix.vec3.fromValues(positions[index * 3], positions[index * 3 + 1], positions[index * 3 + 2]);

        minX = Math.min(positions[index * 3], minX);
        maxX = Math.max(positions[index * 3], maxX);

        minY = Math.min(positions[index * 3 + 1], minY);
        maxY = Math.max(positions[index * 3 + 1], maxY);

        minZ = Math.min(positions[index * 3 + 2], minZ);
        maxZ = Math.max(positions[index * 3 + 2], maxZ);
        points.push(vertex);
        facet_indices.push(index);
    }

    const v1 = glMatrix.vec3.subtract(glMatrix.vec3.create(), points[1], points[0]);
    const v2 = glMatrix.vec3.subtract(glMatrix.vec3.create(), points[2], points[0]);
    const cross = glMatrix.vec3.cross(glMatrix.vec3.create(), v1, v2);
    const normal = glMatrix.vec3.normalize(glMatrix.vec3.create(), cross);

    for (let i of facet_indices) {
        normals[i * 3] += normal[0];
        normals[i * 3 + 1] += normal[1];
        normals[i * 3 + 2] += normal[2];
    }
}
let normalBuffer = createGPUBuffer(device, normals, GPUBufferUsage.VERTEX);

노멀은 삼각형 두 모서리의 외적을 사용하여 계산됩니다.

@group(0) @binding(0)
var modelView: mat4x4;
@group(0) @binding(1)
var projection: mat4x4;
@group(0) @binding(2)
var normal: mat4x4;

셰이더 코드에서는 노멀을 위한 별도의 변환 행렬인 노멀 변환이라는 새로운 유니폼을 도입합니다. 이 변환 행렬은 기하학적 형상에 적용되는 동일한 모델뷰 행렬에서 파생되었지만, 노멀 변환에 모델뷰 행렬을 단순히 사용할 수는 없습니다.

비균일 스케일링 하에서 노멀의 2D 그림

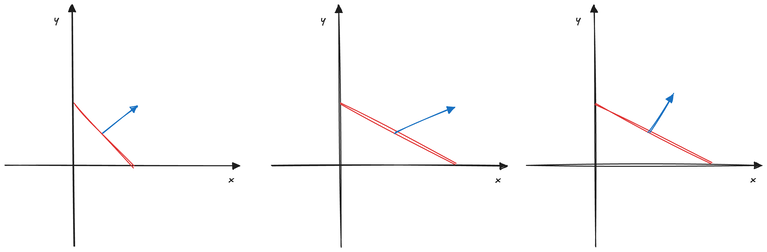
이 별도의 변환이 필요한 이유를 이해하는 것이 이 튜토리얼의 핵심 내용입니다. 2D 그림을 사용하여 설명해 보겠습니다. 선과 그 노멀이 있고, 여기에 변환을 적용한다고 상상해 봅시다. 변환이 평행 이동, 회전, 그리고 균일 스케일링만 포함하는 한, 동일한 변환 하에서 노멀은 변환된 선에 수직으로 유지되어야 합니다. 그러나 비균일 스케일링이 포함되는 경우에는 그렇지 않습니다. 예를 들어, 선을 x축을 따라만 늘리면, 동일한 늘림 하에서의 새 노멀은 더 이상 선에 수직이 아닙니다. 결과적으로, 변환 후에도 노멀이 표면에 수직으로 유지되도록 하는 노멀에 대한 다른 변환을 찾아야 합니다.

이를 수학적으로 이해하기 위해, 두 벡터 v와 n을 고려해 봅시다. 여기서 v는 원본 표면의 탄젠트 벡터이고 n은 원본 표면 노멀입니다. 이들은 수직성으로 인해 다음 관계를 보입니다:

v \times n^\intercal = 0

우리는 MM^{-1} = \mathbb{I}임을 알고 있으며, 여기서 \mathbb{I}는 단위 행렬입니다. 이를 위 식에 포함하면 다음과 같습니다:

\begin{aligned} v \times n^\intercal &= 0 \\ v \times M \times M^{-1} \times n^\intercal &= 0 \\ v \times M \times (n \times M^{-1\intercal})^\intercal &= 0 \end{aligned}

v \times M이 변환된 탄젠트 벡터를 나타내므로, 이를 v^\prime라고 표기하겠습니다. 우리는 v^\prime \times (n^\prime)^\intercal = 0임을 알고 있으며, 여기서 n^\prime는 변환된 노멀입니다. 따라서 다음과 같이 추론할 수 있습니다:

n^\prime = n \times M^{-1\intercal}

그러므로 M^{-1\intercal}는 우리가 찾는 노멀 변환 행렬이며, 이는 모델뷰 행렬의 역행렬의 전치입니다. 적절한 노멀 변환 행렬을 도출했으므로, 해당 셰이더 코드를 살펴보겠습니다:

struct VertexOutput {
    @builtin(position) clip_position: vec4,
    @location(0) normal: vec3
};

@vertex
fn vs_main(
    @location(0) inPos: vec3,
    @location(1) inNormal: vec3
) -> VertexOutput {
    var out: VertexOutput;
    out.clip_position = projection * modelView * vec4(inPos, 1.0);
    out.normal = normalize(normal * vec4(inNormal, 0.0)).xyz;
    return out;
}

정점 단계 진입점에서는 @location(1)에 inNormal이라는 새로운 정점 속성을 도입합니다. 이 속성은 표면 노멀을 나타내는 세 개의 부동 소수점 값 벡터입니다. 이 입력에 노멀 변환을 적용하고, 결과로 변환된 노멀은 일반적으로 조명 계산이 수행되는 프래그먼트 셰이더로 전달됩니다.

@fragment
fn fs_main(in: VertexOutput,  @builtin(front_facing) face: bool) -> @location(0) vec4 {
    if (face) {
        var normal:vec3 = normalize(in.normal);
        return vec4(normal ,1.0);
    }
    else {
        return vec4(0.0, 1.0, 0.0 ,1.0);
    }
}

노멀은 일반적으로 프래그먼트 셰이더 내의 렌더링 알고리즘에서 활용됩니다. 그러나 아직 조명이나 노멀과 관련된 다른 복잡한 렌더링 알고리즘을 논의하지 않았으므로, 이 튜토리얼에서는 단순히 색상으로 렌더링하여 노멀을 시각화할 것입니다. 래스터화 과정 중 보간이 벡터의 길이에 영향을 미칠 수 있으므로 먼저 노멀 벡터를 정규화합니다. 정의상 노멀은 방향을 나타내므로 항상 단위 벡터입니다. 이 색상 기반 시각화는 표면 전체에 걸친 노멀의 분포를 이해하는 데 도움이 됩니다.

const normalAttribDesc = {
    shaderLocation: 1, // @location(1)
    offset: 0,
    format: 'float32x3'
};

const normalBufferLayoutDesc = {
    attributes: [normalAttribDesc],
    arrayStride: 4 * 3, // sizeof(float) * 3
    stepMode: 'vertex'
};

이제 JavaScript 코드로 넘어가서 노멀 속성 디스크립터를 소개합니다. 이 디스크립터는 위치 속성 디스크립터와 유사하지만, 셰이더 코드에서 노멀에 대해 정의한 @location(1)에 해당하도록 shaderLocation을 1로 지정합니다.

const pipelineDesc = {
    layout,
    vertex: {
        module: shaderModule,
        entryPoint: 'vs_main',
        buffers: [positionBufferLayoutDesc, normalBufferLayoutDesc]
    },
    fragment: {
        module: shaderModule,
        entryPoint: 'fs_main',
        targets: [colorState]
    },
    primitive: {
        topology: 'triangle-list',
        frontFace: 'ccw',
        cullMode: 'none'
    },
    depthStencil: {
        depthWriteEnabled: true,
        depthCompare: 'less',
        format: 'depth24plus-stencil8'
    }
};

파이프라인 디스크립터를 정의할 때, 위치 버퍼와 노멀 버퍼를 모두 정점 버퍼로 제공해야 합니다. 따라서 렌더링 과정에서 두 개의 정점 버퍼를 설정해야 합니다.

노멀로 채색된 찻주전자

이제 찻주전자를 렌더링해 봅시다. 시각화하면 찻주전자 표면이 생생한 색상 스펙트럼을 나타내는 것을 볼 수 있습니다. 이 색상은 표면 각 지점의 노멀 방향에 해당합니다. 노멀을 정점 수준에서 정의했고 GPU가 정점 버퍼에서 프래그먼트 셰이더로의 보간을 처리하므로, 찻주전자 표면의 색상 전환이 놀랍도록 부드럽게 나타납니다. 눈에 띄는 삼각형이나 날카로운 모서리가 없어 이 기술의 효과를 입증합니다. 이러한 노멀의 부드러운 전환은 더 복잡한 렌더링 시나리오에서 사실적이고 매끄러운 조명 효과를 달성하는 데 중요합니다.