1.8 변환 행렬 활용하기

이번 튜토리얼에서는 이전 셰이더 예제를 다시 방문하여 동일한 결과인 오프셋 삼각형을 달성할 것입니다. 그러나 이번에는 단순한 오프셋 벡터 대신 변환 행렬을 사용할 것입니다. 정점 위치에 이 변환 행렬을 곱함으로써 동일한 결과를 얻을 수 있습니다. 핵심은 오프셋 벡터를 추가하는 것이 변환 행렬을 적용하는 것과 동일하다는 것입니다.

변환 행렬은 변환을 나타내는 데 더 다재다능한 방법을 제공합니다. 실제 애플리케이션에서는 오프셋만 적용하는 경우가 드뭅니다. 이러한 행렬은 오프셋뿐만 아니라 스케일링, 회전 및 투영까지 처리할 수 있습니다. 실제로 변환 행렬은 정점 위치를 조작하는 가장 일반적인 방법입니다. 그래픽스 개발자를 지망하는 사람들에게는 변환 행렬에 대한 철저한 이해가 중요합니다. 이는 그래픽스 프로그래밍의 피할 수 없는 측면입니다.

그래픽스 개발이 처음이라면 이 개념이 어렵게 느껴질 수 있습니다. 단계별로 접근하여 이를 이해해 봅시다. 2D 예제와 구체적인 시나리오부터 시작하겠습니다. 이 튜토리얼에서는 스케일링, 변환 및 회전에 중점을 둘 것입니다. 투영 행렬은 다음 장에서 살펴볼 것입니다.

스케일링

스케일링은 이해하기 가장 간단한 변환입니다. 2D 벡터 (x,y)가 있다고 상상해 보세요. 이 벡터를 3배로 스케일링하려면 늘어난 벡터는 (3x,3y)가 됩니다. x와 y에 다른 곱셈자를 적용할 수 있습니다. 예를 들어, (3,4)를 사용하면 (3x,4y)가 됩니다. 2D 스케일링 공식은 간단합니다:

\begin{aligned} x^\prime &= 3 \times x \\ y^\prime &= 4 \times y \\ \end{aligned}

이 계산을 덜 직관적인 행렬 곱셈 형태로 다시 작성할 수 있습니다. 이 튜토리얼이 끝날 때쯤에는 컴퓨터 그래픽스에서 행렬이 변환을 나타내는 선호되는 방법인 이유를 이해하게 될 것입니다.

\begin{pmatrix} 3 & 0 \\ 0 & 4 \end{pmatrix} \times \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 3x \\ 4y \end{pmatrix}

이 계산은 3D 공간으로 쉽게 확장됩니다:

\begin{pmatrix} 3 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 5 \end{pmatrix} \times \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 3x \\ 4y \\ 5z \end{pmatrix}

변환

변환은 약간 더 복잡합니다. 다시 2D부터 시작하겠습니다. 2D 점 (x,y)를 (3,4)만큼 오프셋하려면 새로운 점을 다음과 같이 계산합니다:

\begin{aligned} x^\prime &= 3 + x \\ y^\prime &= 4 + y \\ \end{aligned}

이를 행렬 곱셈으로 다시 작성하는 것은 즉시 명확하지 않습니다. 시도해 볼 수 있습니다:

\begin{pmatrix} 1 & \frac{3}{y} \\ \frac{4}{x} & 1 \end{pmatrix} \times \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x + 3 \\ 4 + y \end{pmatrix}

이것은 작동하지만, 변환 행렬이 원하는 오프셋뿐만 아니라 벡터 (x,y)에도 연결되기 때문에 이상적이지 않습니다. 벡터를 알지 못하면 변환 행렬을 유도할 수 없습니다. 이는 그래픽스 애플리케이션에서 바람직하지 않습니다. 변환 행렬을 한 번 정의하고 이를 어떤 정점에든 적용하여 정점의 실제 위치에 관계없이 동일한 변환을 생성하기를 원하기 때문입니다.

변환 행렬이 오프셋에만 의존하도록 하는 영리한 트릭을 사용할 수 있습니다:

\begin{pmatrix} 1 & 0 & 3 \\ 0 & 1 & 4 \\ 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + 3 \\ y + 4 \\ 1 \end{pmatrix}

여기서 행렬을 3x3으로 확장하고, 오프셋은 마지막 열에 정의됩니다. 또한 점의 위치를 3x1 벡터로 확장하여 행렬과 계속 곱할 수 있도록 합니다. 이제 변환 행렬은 오프셋에만 관련되며, 이를 벡터에 곱하면 (x+3, y+4, 1)이 생성되며, 여기서 처음 두 요소는 오프셋된 2D 점을 나타냅니다.

이 접근 방식은 추가 데이터와 계산을 추가하는 것처럼 보이지만, 우리가 원하는 속성을 가진 행렬을 만듭니다. 2D 스케일링 행렬을 3x3으로 확장하여 변환 행렬과 동일한 형태를 갖도록 수정할 수도 있습니다.

이를 3D로 확장하는 것은 간단합니다. 단순히 4x4 행렬을 사용합니다:

\begin{pmatrix} 1 & 0 & 0 & 3 \\ 0 & 1 & 0 & 4 \\ 0 & 0 & 1 & 5 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} x \\ y \\ z \\ 1 \end{pmatrix} = \begin{pmatrix} x + 3 \\ y + 4 \\ z + 5 \\ 1 \end{pmatrix}

회전

회전은 개념화하기 가장 어려운 변환입니다. 각도 \theta만큼 회전하려는 2D 벡터 (x,y)가 있다고 상상해 보세요. 먼저 (x,y)가 단위 벡터라고 가정하고 수동으로 회전을 계산해 봅시다. 그런 다음 임의의 길이 벡터를 회전하는 방법을 고려할 것입니다.

2D 벡터 (X,Y)를 각도 Θ만큼 회전시키기

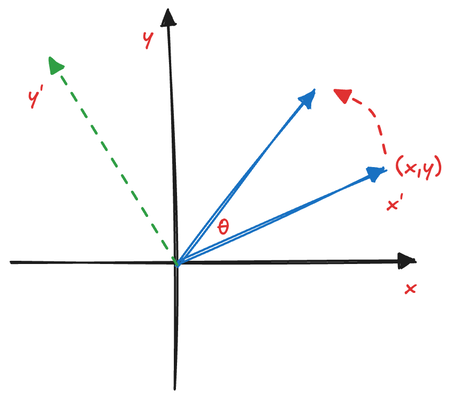
벡터를 \theta만큼 회전시키려면 (x,y)가 x^\prime축이고 (-y, x)가 y^\prime축인 새로운 좌표계를 구성할 수 있습니다. 이 새로운 시스템에서 회전된 벡터와 x^\prime축은 각도 \theta를 이룹니다.

새로운 좌표계에서 회전된 벡터의 위치는 (cos(\theta)x^\prime, sin(\theta)y^\prime)입니다. x^\prime를 (x,y)로, y^\prime를 (-y,x)로 대체하면 원래 좌표계에서 새로운 벡터인 (cos(\theta)x-sin(\theta)y, cos(\theta)y+sin(\theta)x)를 얻습니다.

이 계산을 행렬 곱셈으로 다시 작성할 수 있습니다:

\begin{pmatrix} cos(\theta) & -sin(\theta) \\ sin(\theta) & cos(\theta) \end{pmatrix} \times \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} cos(\theta)x - sin(\theta)y\\ sin(\theta)x + cos(\theta)y \end{pmatrix}

단위 벡터가 아닌 경우, 길이 l = \sqrt{x^2+y^2}로 정규화한 다음 회전하고 다시 스케일링할 수 있습니다. 회전 행렬은 벡터 크기와 무관하며 회전 각도에만 관련된다는 것을 알 수 있습니다.

이러한 계산을 행렬 곱셈으로 다시 작성하는 우리의 목표는 계산 형식을 통합하는 것입니다. 어떤 변환이든 행렬 곱셈을 통해 달성할 수 있습니다. 이를 통해 여러 행렬을 벡터와 곱하여 여러 변환을 쉽게 연결할 수 있습니다. 각 행렬은 하나의 변환을 나타내며, 일련의 변환 행렬을 곱셈을 통해 단일 행렬로 병합할 수 있습니다. 이 속성은 3D 공간의 회전 행렬을 유도하는 데 중요합니다.

xy 평면에 대한 회전 행렬을 유도했으므로, 이를 xz 및 yz 평면으로 쉽게 확장할 수 있습니다. 3D 공간의 어떤 복잡한 회전도 각 평면에서 세 단계의 회전으로 분해될 수 있습니다. 각도 \theta_{xy}, \theta_{xz}, \theta_{yz}를 가정하면, 3D 회전 행렬은 다음과 같습니다:

\begin{pmatrix} 1 & 0 & 0 \\ 0 & cos(\theta_{yz}) & -sin(\theta_{yz}) \\ 0 & sin(\theta_{yz}) & cos(\theta_{yz}) \end{pmatrix} \times \begin{pmatrix} cos(\theta_{xz}) & 0 & -sin(\theta_{xz}) \\ 0 & 1 & 0 \\ sin(\theta_{xz}) & 0 & cos(\theta_{xz}) \end{pmatrix} \times \begin{pmatrix} cos(\theta_{xy}) & -sin(\theta_{xy}) & 0 \\ sin(\theta_{xy}) & cos(\theta_{xy}) & 0 \\ 0 & 0 & 1 \end{pmatrix}

이 세 가지 유형의 변환 행렬을 사용하면 투영을 제외한 거의 모든 변환을 수행할 수 있습니다. 예를 들어, 원근 투영은 실제 경험과 일치하게 멀리 있는 객체가 가까운 객체보다 작게 보이도록 합니다. 이 변형은 회전, 변환 및 스케일링만으로는 달성할 수 없습니다. 3D 그래픽스에서 카메라를 구현하는 데 중요하므로 다음 장에서 투영을 자세히 살펴볼 것입니다.

동차 좌표

스케일링과 회전에만 관심을 가졌다면 3x3 행렬로 충분했을 것입니다. 그러나 변환을 포함하려면 행렬을 4x4로, 벡터를 4x1로 확장해야 합니다. 이전 셰이더 코드에서 정점 셰이더의 위치 출력이 항상 vec4였고, 네 번째 요소가 1.0으로 설정되었음을 기억하십시오. 이제 그 이유를 이해하셨을 것입니다. 이러한 4D 벡터를 동차 좌표라고 합니다. 네 번째 요소는 항상 1이 아니라, 점의 경우 1이고 벡터의 경우 0입니다. 이 구별은 중요합니다. 왜냐하면 항상 원점에서 시작하는 벡터는 스케일링되거나 회전될 수 있지만 변환될 수는 없기 때문입니다. 네 번째 요소를 0으로 설정하면 벡터가 어떤 변환 행렬에서도 변환의 영향을 받지 않도록 보장합니다.

네 번째 요소가 1 또는 0이 아닐 때, 그 값은 스케일링 계수로 처리됩니다. 점의 실제 위치는 (\frac{x}{w},\frac{y}{w},\frac{z}{w})로 얻을 수 있습니다.

이제 변환 행렬 이론을 소개했으니, 실제 구현을 살펴보겠습니다. 변환 행렬 외에도 glMatrix라는 유용한 타사 라이브러리를 소개할 것입니다. 2D 점에 대한 변환 행렬을 수동으로 만드는 것은 그리 어렵지 않지만, 3D 점의 경우 매우 번거롭습니다. 여기서 glMatrix가 매우 유용합니다. 이 라이브러리는 변환 행렬을 생성하고 컴퓨터 그래픽스에서 광범위하게 사용되는 다양한 벡터 및 행렬 관련 계산을 처리할 수 있습니다. 우리는 이 책 전체에서 이 라이브러리에 의존할 것입니다.

@group(0) @binding(0)
var transform: mat4x4;

@vertex
fn vs_main(
    @location(0) inPos: vec3,
    @location(1) inTexCoords: vec2
) -> VertexOutput {
    var out: VertexOutput;
    out.clip_position = transform * vec4(inPos, 1.0);
    out.tex_coords = inTexCoords;
    return out;
}

셰이더 코드를 업데이트하여 offset이라는 vec3 유니폼을 mat4x4 타입의 transform이라는 새 유니폼으로 교체했습니다. 이 변경은 클립 위치를 계산하는 방식을 변경합니다. 이전 버전에서는 inPos 변수를 offset 벡터에 추가하여 최종 위치를 결정했습니다. 이제 inPos 벡터에 변환 행렬을 직접 곱하여 이를 달성합니다.

let translateMatrix = glMatrix.mat4.fromTranslation(glMatrix.mat4.create(), glMatrix.vec3.fromValues(-0.5, -0.5, 0.0));

let uniformBuffer = createGPUBuffer(device, translateMatrix, GPUBufferUsage.UNIFORM);

유니폼 버퍼 설정을 살펴보겠습니다. 대부분은 비슷하지만, 주요 차이점은 변환 행렬을 생성하는 방식에 있습니다.

변환이 이동만 포함하므로 glMatrix 라이브러리의 fromTranslation 헬퍼 함수를 사용합니다. 이 라이브러리는 vec2 및 mat4와 같은 다양한 차원의 벡터 및 행렬 유틸리티를 포괄적으로 제공합니다. 각 유형에 대해 대수 계산을 수행하거나 필요에 맞게 값을 구성하는 수많은 함수를 제공합니다. 예를 들어, fromTranslation은 오프셋 벡터를 기반으로 새 행렬을 생성하고, fromRotation은 회전을 정의하는 행렬을 생성합니다. 또한 fromRotationTranslation은 회전과 변환을 모두 결합한 행렬을 생성할 수 있습니다.

JavaScript 이외의 다른 프로그래밍 언어에 익숙하다면 glMatrix의 구문이 다소 장황하다고 느낄 수 있습니다. 이 장황함은 주로 JavaScript에 연산자 오버로딩이 없기 때문에 발생합니다. 그러나 glMatrix에 익숙해지면 이 추가적인 장황함은 더 이상 문제가 되지 않습니다.

생성된 변환 행렬에 관심이 있다면 해당 값을 출력하여 이를 정점에 곱하면 실제로 원하는 오프셋을 달성하는지 수동으로 확인할 수 있습니다.

나머지 코드는 크게 변경되지 않습니다. 유니폼 버퍼를 생성하고 편리한 헬퍼 함수 createGPUBuffer를 사용하여 변환 행렬의 내부 값(16개의 float)을 이 버퍼로 복사합니다.

코드를 실행하면 동일한 오프셋 삼각형을 볼 수 있습니다. fromTranslation 함수의 입력을 변경하여 다른 변환 행렬을 유도해 보세요. 또한 fromRotationTranslation 함수를 사용하여 삼각형을 회전할 수 있는지 실험해 볼 수도 있습니다.

이 장의 샘플 코드는 비교적 기본적이지만, 핵심은 변환 행렬을 이해하는 데 있습니다. 이후 장에서는 이 개념이 다양한 시나리오에 광범위하게 적용되는 것을 보게 될 것입니다.